Friday, November 27, 2009
Saturday, November 21, 2009
Grad School Applications
As of today, I have applied to four graduate schools. I've finished the online applications for all four, submitted my Statement of Purpose (except to one school, pending an email inquiry), sent my GRE scores, and emailed instructions to my professors on how they can send/submit their letters of recommendation for me.
I can't send my transcripts from Metro until the semester ends, because I need those grades on there, and that will be mid/late December, which is in time for all of the deadlines, but still makes me feel a little bit nervous. I don't want to send my other transcripts until then either, because I don't want them to be looking at all my crappy older grades without the better, newer grades. (That's probably just irrational, but whatever.)
I still have five more schools to finish my applications to, but I'm glad that I've made progress and have some apps in. I still have no idea how good or bad a candidate I am; I can't tell if I'll be lucky to even sneak into my lowest-rated programs or if I can expect several programs to invite me. But all I can do at this point is apply and wait.
I can't send my transcripts from Metro until the semester ends, because I need those grades on there, and that will be mid/late December, which is in time for all of the deadlines, but still makes me feel a little bit nervous. I don't want to send my other transcripts until then either, because I don't want them to be looking at all my crappy older grades without the better, newer grades. (That's probably just irrational, but whatever.)
I still have five more schools to finish my applications to, but I'm glad that I've made progress and have some apps in. I still have no idea how good or bad a candidate I am; I can't tell if I'll be lucky to even sneak into my lowest-rated programs or if I can expect several programs to invite me. But all I can do at this point is apply and wait.
Thursday, November 19, 2009
Math Gaps
I read something recently where a person was talking about her approach to teaching math - that she reassures her class that they are not "bad" at math, but that somewhere along the way, they had a bad teacher, or they missed a day, and the lacking knowledge accumulated so that now they are confused by various things. And I was thinking of how many gaps I have in my own knowledge of math, and how crazy these gaps drive me when they show up.
It's hard to even recognize that something is caused by a gap. A certain topic will show up (infinite series, say, or rules of limits) and my mind will just go "that's too hard" or "I can't do those" without asking why. Are these topics somehow such that I alone cannot learn them? Do I have some tiny genetic flaw that has knocked out the part of my mind that would let me understand what a Taylor series is?
No. I just don't understand something because I have some gaps, and the thing to do, then, if I'm serious about math, is to figure out what the gaps are and fill them in. It's unlikely I'm missing anything that I can't learn, so I need to just get on that, as it comes up. And now that I'm finally more of a badass about reading and understanding math, I'm in a perfect position to do so.
It's hard to even recognize that something is caused by a gap. A certain topic will show up (infinite series, say, or rules of limits) and my mind will just go "that's too hard" or "I can't do those" without asking why. Are these topics somehow such that I alone cannot learn them? Do I have some tiny genetic flaw that has knocked out the part of my mind that would let me understand what a Taylor series is?
No. I just don't understand something because I have some gaps, and the thing to do, then, if I'm serious about math, is to figure out what the gaps are and fill them in. It's unlikely I'm missing anything that I can't learn, so I need to just get on that, as it comes up. And now that I'm finally more of a badass about reading and understanding math, I'm in a perfect position to do so.
Monday, November 16, 2009
Gendered Language
Sometimes my grandmother used to tell me, "Act like a little lady," and it always rankled me. Even when I was four years old I didn't like the word "lady" and didn't want to be one. But it strikes me that I have an unusual aversion to unnecessarily gendered language.
I noticed right away that my new therapist tended to say things like, "You're clearly a very [adjective] woman," and that it rubbed me completely the wrong way, even though the adjectives were positive things like "intelligent" or "passionate." (I mentioned it and he seems to have stopped.)
I never say things like "when I was a little girl" -- it's always "kid" or "child." I don't think I ever refer to myself as a woman unless there are situations that clearly call for it ("I'm not sure how other women manage their facial hair").
I found myself saying the other day that Ed would probably not be a good partner for the type of person who prefers not to know certain things. I don't think Ed will ever date a man, so I'm not sure why the language is gender-neutral except that "the type of woman who prefers not to know certain things" seems slightly offensive to me, like it invokes a stereotype, while "type of person" does not.
I don't think it's only female gender that I tend not to specify. I would never say, "What were you like as a little boy?" instead of "kid." I wouldn't call someone a sensitive, smart, fair, or caring "man" instead of "person." (I would only use "man" if I intended a constrast, e.g., "You're a really maternal man," and even then I'd probably say "person" most of the time.)
I don't do this gender-neutrality on purpose, I don't think. I use common words like "waitress" and "actress" and "handyman." I certainly use pronounce like "he" and "she" in the normal way (though I'm also a fan of the unfairly-maligned singular "they").
I wonder if this is a function of my feminism (using the word in a very basic sense to incorporate the feminism I already had when I was 4 years old), something that is more accepted in my social environment, or a result of some personality trait.
I noticed right away that my new therapist tended to say things like, "You're clearly a very [adjective] woman," and that it rubbed me completely the wrong way, even though the adjectives were positive things like "intelligent" or "passionate." (I mentioned it and he seems to have stopped.)
I never say things like "when I was a little girl" -- it's always "kid" or "child." I don't think I ever refer to myself as a woman unless there are situations that clearly call for it ("I'm not sure how other women manage their facial hair").
I found myself saying the other day that Ed would probably not be a good partner for the type of person who prefers not to know certain things. I don't think Ed will ever date a man, so I'm not sure why the language is gender-neutral except that "the type of woman who prefers not to know certain things" seems slightly offensive to me, like it invokes a stereotype, while "type of person" does not.
I don't think it's only female gender that I tend not to specify. I would never say, "What were you like as a little boy?" instead of "kid." I wouldn't call someone a sensitive, smart, fair, or caring "man" instead of "person." (I would only use "man" if I intended a constrast, e.g., "You're a really maternal man," and even then I'd probably say "person" most of the time.)
I don't do this gender-neutrality on purpose, I don't think. I use common words like "waitress" and "actress" and "handyman." I certainly use pronounce like "he" and "she" in the normal way (though I'm also a fan of the unfairly-maligned singular "they").
I wonder if this is a function of my feminism (using the word in a very basic sense to incorporate the feminism I already had when I was 4 years old), something that is more accepted in my social environment, or a result of some personality trait.
Friday, November 13, 2009
Idiot David Lane
So, Richard Heene pled guilty today to a felony. He's the guy who, along with his family, engineered the hoax that caused a big rescue operation to save his son who was supposed to have accidentally taken off in a helium balloon, but who was actually hiding in the garage as instructed by his parents. A lot of Americans watched this rescue effort anxiously, including some people in my office.
From the Denver Post article, we get this:
From the Denver Post article, we get this:
After the hearing, Richard Heene's attorney David Lane said that the seriousness of the charges reflects the anger Americans felt after learning they had been duped by the parents into fearing for Falcon's safety.I can't believe the man's lawyer would say something so offensive and unprofessional. It is not "emotional instability" that causes people to become angry when they've been tricked into fearing for a young child's life, or to want restitution for a foolish crime that wasted public money on an unnecessary rescue operation.
"Don't mess with America's emotions," Lane said. "America has the emotional instability of a hormonal teenager."
Thursday, November 12, 2009
Thomae's Function and Integrability
Thomae's Function is something we've discussed in advanced calc a few times - it's basically a sort of pathological function that is discontinuous at every rational number. I've drawn a picture here, along with the definition:
 For irrational numbers, the value of f(x) is zero, and for rational numbers (other than 0), it's 1 over the denominator in reduced terms, so for instance f(1/5) = f(2/5) = f(3/5) = 1/5.
For irrational numbers, the value of f(x) is zero, and for rational numbers (other than 0), it's 1 over the denominator in reduced terms, so for instance f(1/5) = f(2/5) = f(3/5) = 1/5.
Between any two real numbers, there is a rational number, and between any two real numbers, there is an irrational number, so there are two things to notice here, to wit:
When Newton and Leibniz invented caculus, they conceived of integration solely as using antiderivatives. That is, if you have two functions, F and f, such that the slope of F at a point x is the value of f(x) -- i.e., F'(x) = f(x) -- then f is the derivative of F, and F is the antiderivative of f. By the Fundamental Theorem of Calculus, you can use an antiderivative to calculate a definite integral of f - that is, to find the area under the f(x) curve between two points (the area of S in this picture):
 Now, obviously, you can't conceive of integration in quite the same way for something like Thomae's function. It can't possibly have an antiderivative - even if you can make a function with that kind of infinitely discontinuous slope, which I can't imagine you could, it wouldn't have a derivative.
Now, obviously, you can't conceive of integration in quite the same way for something like Thomae's function. It can't possibly have an antiderivative - even if you can make a function with that kind of infinitely discontinuous slope, which I can't imagine you could, it wouldn't have a derivative.
So in the 19th century, a different way of conceiving of integrals was conceived. In calculus, you learn about Riemann sums. Basically, if you divide the area under the curve into vertical boxes, and then calculate the area of each box, that's an approximation of the area under the curve. The more boxes you have, the closer your approximation gets to the actual value, and the limit of those approximations is the area under the curve, as in this picture:
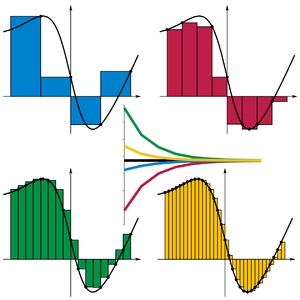 It turns out that using a method similar to this, Thomae's function can be integrated on the interval [0, 1]. The method is called "Darboux Sums."
It turns out that using a method similar to this, Thomae's function can be integrated on the interval [0, 1]. The method is called "Darboux Sums."
One question when you use Riemann sums is how to calculate the height of each box. An easy way to do it is to use the leftmost or rightmost edge of the box as the height. As long as you use some method, it actually doesn't really matter what it is -- the approximations will still get better and better -- but Darboux does it a particular way.
Specifically, for Darboux sums you get an upper sum and a lower sum. For the upper sum, you use, as the height of each box, the highest value inside of that box, and for the lower sum, you use the lowest value inside of each box. You then add up the areas of all of the boxes, and that gives you an upper sum and a lower sum for the integral.
What next? Darboux's Criterion for Integrability is a theorem that says that if, given an error amount (epsilon), there is a way to divide up the function (i.e., a placement of the boxes - they don't all have to be the same width) such that the difference between the upper and lower sums is less than epsilon, the function is integrable.
If we apply this method to Thomae's function, no matter how we partition the function, the lower Darboux sum will always be 0, because every interval will contain irrational numbers. Since, if it's integrable, the upper sum has be able to be made arbitrarily close to the lower sum, it's clear that, if we can integrate Thomae's function on [0, 1], the result (the area under the "curve," if you will) must be 0.
And it turns out that we can indeed get the upper sum to be as close as we want to 0 (though never actually 0 - but that is never required in calculus, which deals in limits). I won't go through the proof of that, but it relies on the fact that, basically, if you draw a horizontal line somewhere above 0 in this function, there will only be a finite number of points above that line. Then you can just make the boxes that contain those points skinny enough that their overall area is arbitrarily low, and there you go.
 For irrational numbers, the value of f(x) is zero, and for rational numbers (other than 0), it's 1 over the denominator in reduced terms, so for instance f(1/5) = f(2/5) = f(3/5) = 1/5.
For irrational numbers, the value of f(x) is zero, and for rational numbers (other than 0), it's 1 over the denominator in reduced terms, so for instance f(1/5) = f(2/5) = f(3/5) = 1/5.Between any two real numbers, there is a rational number, and between any two real numbers, there is an irrational number, so there are two things to notice here, to wit:
- the x-axis is extra black because there are infinite irrational points on this interval [0, 1] that are irrational so that f(x) = 0
- points below 0.1 on the y axis aren't shown, but would continue this sort of ever-thickening pyramid structure all the way down
When Newton and Leibniz invented caculus, they conceived of integration solely as using antiderivatives. That is, if you have two functions, F and f, such that the slope of F at a point x is the value of f(x) -- i.e., F'(x) = f(x) -- then f is the derivative of F, and F is the antiderivative of f. By the Fundamental Theorem of Calculus, you can use an antiderivative to calculate a definite integral of f - that is, to find the area under the f(x) curve between two points (the area of S in this picture):
 Now, obviously, you can't conceive of integration in quite the same way for something like Thomae's function. It can't possibly have an antiderivative - even if you can make a function with that kind of infinitely discontinuous slope, which I can't imagine you could, it wouldn't have a derivative.
Now, obviously, you can't conceive of integration in quite the same way for something like Thomae's function. It can't possibly have an antiderivative - even if you can make a function with that kind of infinitely discontinuous slope, which I can't imagine you could, it wouldn't have a derivative.So in the 19th century, a different way of conceiving of integrals was conceived. In calculus, you learn about Riemann sums. Basically, if you divide the area under the curve into vertical boxes, and then calculate the area of each box, that's an approximation of the area under the curve. The more boxes you have, the closer your approximation gets to the actual value, and the limit of those approximations is the area under the curve, as in this picture:
 It turns out that using a method similar to this, Thomae's function can be integrated on the interval [0, 1]. The method is called "Darboux Sums."
It turns out that using a method similar to this, Thomae's function can be integrated on the interval [0, 1]. The method is called "Darboux Sums."One question when you use Riemann sums is how to calculate the height of each box. An easy way to do it is to use the leftmost or rightmost edge of the box as the height. As long as you use some method, it actually doesn't really matter what it is -- the approximations will still get better and better -- but Darboux does it a particular way.
Specifically, for Darboux sums you get an upper sum and a lower sum. For the upper sum, you use, as the height of each box, the highest value inside of that box, and for the lower sum, you use the lowest value inside of each box. You then add up the areas of all of the boxes, and that gives you an upper sum and a lower sum for the integral.
What next? Darboux's Criterion for Integrability is a theorem that says that if, given an error amount (epsilon), there is a way to divide up the function (i.e., a placement of the boxes - they don't all have to be the same width) such that the difference between the upper and lower sums is less than epsilon, the function is integrable.
If we apply this method to Thomae's function, no matter how we partition the function, the lower Darboux sum will always be 0, because every interval will contain irrational numbers. Since, if it's integrable, the upper sum has be able to be made arbitrarily close to the lower sum, it's clear that, if we can integrate Thomae's function on [0, 1], the result (the area under the "curve," if you will) must be 0.
And it turns out that we can indeed get the upper sum to be as close as we want to 0 (though never actually 0 - but that is never required in calculus, which deals in limits). I won't go through the proof of that, but it relies on the fact that, basically, if you draw a horizontal line somewhere above 0 in this function, there will only be a finite number of points above that line. Then you can just make the boxes that contain those points skinny enough that their overall area is arbitrarily low, and there you go.
Wednesday, November 11, 2009
Google Images as Visual Dictionary
One of my favorite ways to use Google lately is to look up things I'm unfamiliar with in Google Images. It doesn't work for straight-up words (like "mendacious"), but it works great for things like "hipster" or "umbros" or "engineer boots." You almost immediately find out what the thing is without the annoying mediation of words.
It's like the best visual dictionary of all time.
It's like the best visual dictionary of all time.
Friday, November 06, 2009
And Then What?
In a recent Since You Asked column, a woman asks, "How can I detach from my mother without feeling like a horrible person?" Cary counsels:
For instance, if I am worried that Ed is mad at me, it can make me very upset. I might then expend mental energy trying to figure out if he is, indeed, angry. Maybe he says he's not, but I think he's lying, or he's angry and doesn't even know it. (A lot of this is hypothetical, but such concerns do come up around some of my other insecurities. For another person, the question might be, "What if he/she is cheating on me?") There's no way to be sure.
I have to stop and say, OK, so he might be angry. What then? Everyone gets angry sometimes. It's not a big deal to have someone angry at you. It's not like he's going to physically attack me. If he yells I'll just wait until he stops, or I can always leave. He probably won't yell anyway. And who is he to be angry? Why do I care? Fuck him if he's mad, I didn't do anything. Whatever.
Sometimes consequences really are pretty catastrophic. What if I have an incurable cancer? The best I can do there is perhaps to consider that I knew I would die of something someday in any case. It's not much comfort. But most fears don't have consequences that are actually that bad. What if I have a panic attack on the airplane? Well, then, I'll feel absolutely horrible for a while, but at some point it will end, and I'll still land on the other side and go on with my life. What if this woman cutting my hair accidentally nicks my ear? Well, it'll hurt a little and then heal.
So I think the key to a lot of those "Oh my god, what if...?" moments is to go ahead and answer the question.
Cognitive therapy lets us ask, OK, so, What if, indeed, I were to feel like a horrible person? What does that really mean? What would be the end result of that? Would I die? Would I feel intense pain? Would others be harmed? Maybe we have had this voice in our heads, this little voice, saying, You can't do that or you'll feel like a horrible person! If we write these thoughts down, and see them, we see that they are not so accurate. We can ask ourselves, OK, how long would I feel like a horrible person? Would it be momentary? Would it last an hour, or days? And just how horrible a person would I feel like?I have discovered lately that this general technique - going down the "what if" path rather than treating it as intolerable - works for a lot of fears. Sometimes it is the key to resolving insecurities.
For instance, if I am worried that Ed is mad at me, it can make me very upset. I might then expend mental energy trying to figure out if he is, indeed, angry. Maybe he says he's not, but I think he's lying, or he's angry and doesn't even know it. (A lot of this is hypothetical, but such concerns do come up around some of my other insecurities. For another person, the question might be, "What if he/she is cheating on me?") There's no way to be sure.
I have to stop and say, OK, so he might be angry. What then? Everyone gets angry sometimes. It's not a big deal to have someone angry at you. It's not like he's going to physically attack me. If he yells I'll just wait until he stops, or I can always leave. He probably won't yell anyway. And who is he to be angry? Why do I care? Fuck him if he's mad, I didn't do anything. Whatever.
Sometimes consequences really are pretty catastrophic. What if I have an incurable cancer? The best I can do there is perhaps to consider that I knew I would die of something someday in any case. It's not much comfort. But most fears don't have consequences that are actually that bad. What if I have a panic attack on the airplane? Well, then, I'll feel absolutely horrible for a while, but at some point it will end, and I'll still land on the other side and go on with my life. What if this woman cutting my hair accidentally nicks my ear? Well, it'll hurt a little and then heal.
So I think the key to a lot of those "Oh my god, what if...?" moments is to go ahead and answer the question.
Thursday, November 05, 2009
Fenceless Confusion
Every Monday and Wednesday when I go to my class in the science building, I park in a corner lot, walk up to and then through the North Classroom building, and when I emerge, walk around the gigantic fence that has surrounded the Science building for probably about two years while they've been working on the new building.
Monday night I came out of North Classroom and...what? Was I in the wrong place? Everything looked different.
Oh. The fence was gone. Amazing! Now you can walk right up to the new science building:

Later, when I came out of class, I headed down the sidewalk, and automatically turned left where the fence has a corner, except...there was still no fence, and I was automatically dodging nothing.
 So I walked over to the new building instead and looked through the windows. They're not quite done finishing the inside, and it's not open yet (to judge by all the signs direly warning you not to go in), but it looks pretty great. One thing I was happy to see was that at least the classrooms I could look in had tables with simple chairs rather than one-piece desks. I find that type of arrangement far more comfortable.
So I walked over to the new building instead and looked through the windows. They're not quite done finishing the inside, and it's not open yet (to judge by all the signs direly warning you not to go in), but it looks pretty great. One thing I was happy to see was that at least the classrooms I could look in had tables with simple chairs rather than one-piece desks. I find that type of arrangement far more comfortable.
Hopefully at least one of my three classes next semester will be in there so I get to experience it before I graduate. It's the least I deserve for having to walk around that fence for years.
Monday night I came out of North Classroom and...what? Was I in the wrong place? Everything looked different.
Oh. The fence was gone. Amazing! Now you can walk right up to the new science building:

Later, when I came out of class, I headed down the sidewalk, and automatically turned left where the fence has a corner, except...there was still no fence, and I was automatically dodging nothing.
 So I walked over to the new building instead and looked through the windows. They're not quite done finishing the inside, and it's not open yet (to judge by all the signs direly warning you not to go in), but it looks pretty great. One thing I was happy to see was that at least the classrooms I could look in had tables with simple chairs rather than one-piece desks. I find that type of arrangement far more comfortable.
So I walked over to the new building instead and looked through the windows. They're not quite done finishing the inside, and it's not open yet (to judge by all the signs direly warning you not to go in), but it looks pretty great. One thing I was happy to see was that at least the classrooms I could look in had tables with simple chairs rather than one-piece desks. I find that type of arrangement far more comfortable.Hopefully at least one of my three classes next semester will be in there so I get to experience it before I graduate. It's the least I deserve for having to walk around that fence for years.
Wednesday, November 04, 2009
Severely Awesome Response
On this Ask MeFi thread, a woman asks
When asked later whether she's objecting to the grammar (e.g., the word order or something) of the statement or the semantics, she clarifies that it's the semantics.
I loved this response by ROU_Xenophobe:
Sometimes my partner says silly things. I forgive him because, after all, we do all have our faults--and mine is leniency. However, sometimes he makes statements like,
"I'm glad I didn't go; if I had gone, and seen hipsters running amok, I would have cried severely."
He uses 'severely' in that fashion ALL THE TIME. I finally took issue with his grammar, & he said that it can mean "to a great degree, or requiring great effort," in which case I put up with him (severely), but that's hardly a good explanation.
I understand that 'severely' is an adverb modifying 'crying.' I still think he's ENTIRELY INCORRECT. MeFi, help a girl out?
When asked later whether she's objecting to the grammar (e.g., the word order or something) of the statement or the semantics, she clarifies that it's the semantics.
I loved this response by ROU_Xenophobe:
I feel that, semantically, one cannot cry severely.I love those examples so hard.
If it's just a light slang usage of a perfectly cromulent word, sure you can.
I mean, say that he was using "thermonuclear" instead. As in, "I would have cried, thermonuclear" or "You hurt me thermonuclear bad." Clearly, he cannot actually cry thermonuclear because his body could not survive converting matter to energy inside his tear ducts.
Or say that he used "level 10" instead. I would have cried level 10. This also can't be, because crying does not involve discrete levels.
Or say he used "filthy." As in "I would have cried filthy" or "I kill you filthy, Vorga." Obviously you can't cry filthy, unless you consider tears to be filth, which is verging on the pathological.
But in all cases you know what he means. He sounds a bit like... dude... but in most circumstances that's not a big deal. If he can speak proper when he needs to, and if he'll stop if this is causing you actual no-shit consternation, all is well.
Wavelets
When I looked up my professor for next semester's "Senior Math Seminar" (the 1-hour class I have on Fridays), I saw that he had written a book about wavelets. And apparently that is going to be the topic for our class, and we'll be using his book.
I don't think I've had a textbook written by my actual professor since...well, Rice. And I only know I had one at Rice because of Jason's famous comment (on a course evaluation he happened to be present for) that the lectures were much better than the textbook (which had been written by the professor). And come to think of it, that may have been Sally's class, so I'm not sure I've ever had this particular experience.
I don't think I've had a textbook written by my actual professor since...well, Rice. And I only know I had one at Rice because of Jason's famous comment (on a course evaluation he happened to be present for) that the lectures were much better than the textbook (which had been written by the professor). And come to think of it, that may have been Sally's class, so I'm not sure I've ever had this particular experience.
Monday, November 02, 2009
Next Semester
I was only going to have two classes (one 3-hour and one 1-hour) next semester, but when I checked the schedule, I saw an opportunity to take Abstract Algebra, which, along with Differential Equations, is one of the most noticeable courses missing from my schooling so far. As of this moment, I am registered for the following classes next semester:
Advanced Calc II (Mon/Wed 7:00-8:15 PM)
This is the continuation of my current class, but unlike my current one, it is 3 hours instead of 4, which will be easier on the schedule.
Abstract Algebra I (Tue/Thu 5:30-6:45 PM)
Yes, once again I will be going to school every day of the week. But wait! There's more!
Senior Mathematics Seminar (Fri 10:00-10:50 AM)
This is a one-hour course required of all math majors. I've looked up past syllabi, and it looks like the professor just picks a topic of some kind and you do projects or something like that. It's convenient that this only meets once, for an hour, and I'm glad it's not on the same day as any of my other classes, but of course it's a bit inconvenient to go to campus in the middle of my morning at work.
Anyway, it should be a fun semester. It's technically 1 less credit hour than I have this semester, despite that I'm taking one more class. We'll see. And, of course, I am supposed to graduate at the end.
Advanced Calc II (Mon/Wed 7:00-8:15 PM)
This is the continuation of my current class, but unlike my current one, it is 3 hours instead of 4, which will be easier on the schedule.
Abstract Algebra I (Tue/Thu 5:30-6:45 PM)
Yes, once again I will be going to school every day of the week. But wait! There's more!
Senior Mathematics Seminar (Fri 10:00-10:50 AM)
This is a one-hour course required of all math majors. I've looked up past syllabi, and it looks like the professor just picks a topic of some kind and you do projects or something like that. It's convenient that this only meets once, for an hour, and I'm glad it's not on the same day as any of my other classes, but of course it's a bit inconvenient to go to campus in the middle of my morning at work.
Anyway, it should be a fun semester. It's technically 1 less credit hour than I have this semester, despite that I'm taking one more class. We'll see. And, of course, I am supposed to graduate at the end.
Subscribe to:
Comments (Atom)




















