Tuesday, August 29, 2006
Pizza
Mosch and I walked over to the store and bought a little packet of pizza crust mix ($0.50; I chose the Kroger brand because it didn't have partially hydrogenated oils) and a bag of shredded mozzarella ($2 or $3; we used half). We already had a jar of spaghetti sauce ($3 for the jar; we used 1/3 of it for the pizza), onions (we used way less than 1/2 of one), and sliced mushrooms (on sale this week for $0.88 for the 8-oz carton; we probably used 2 oz at most).
It took about 10 minutes to prepare the dough according to the package directions. I laid the pizza out on a cookie sheet, not filling the whole sheet. (The other option was to use a 12" pan, so that's about how big the pizza was, I suppose.) 1 cup of sauce, about a cup of mozzarella, and onions & mushrooms as seemed appropriate. 12 minutes later it was done.
I thought it was a pretty excellent pizza for less than $4. Not counting the pleasant stroll to the store and back, it took less time than ordering a pizza and waiting for it to be delivered. Because the crust mix only says to let it rise for 5 minutes, the crust was not puffy/bready/yeasty, but more like a thick cracker (not crispy, just not risen). But it was fine for me. I'm sure you could accomplish the same crust with some flour and yeast and the same amount of effort, which would be even cheaper, and then you could use part or all whole wheat if you wanted.
Thursday, August 24, 2006
Small Multiples
Last week, my boss's boss asked for a chart showing rentals due in Arkansas this year. He said he also wanted a map that would show each month's rentals in a different color. I thought this would create an irritating, confusing map in which patterns would not readily jump out and to read which you'd have to keep glancing back and forth to the legend.
So I decided to try it as small multiples, creating a calendar style map. I also created the map he had asked for, in case he really liked it better. I was hoping the small multiples would be seen as better, but it's hard to separate real needs from "stuff I'm proud of because it's cool and some guy wrote a book about it."
Anyway, both of my immediate bosses liked the calendar version better. Hooray! They like how it really shows that September and October are the big months. Here are the two maps, so you can compare for yourself. I'll do my best to make sure these expand if you click on them.
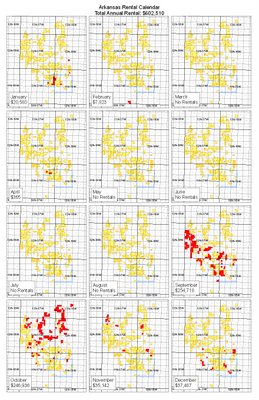
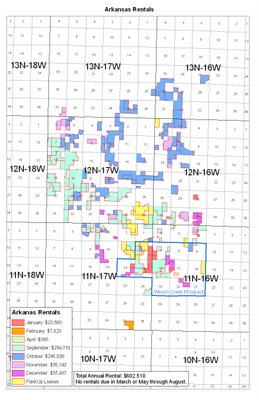
These definitely look better on a large sheet of paper (the original is 11x17, or like two regular sheets of paper side by side), but hopefully these pictures will do them some justice, at least. Obviously if you were really making maps for computer display, neither of these would do.
Stapleton
There have been some fun radio ads about Stapleton houses also. They take the general tone of, do you have some friends who reject suburban life, who like living in a unique house in an older neighborhood, who are willing to put up with not being able to shower and wash dishes at the same time in return for the joys of urban life? Boy have we got a housing development for them! That's the gist, anyway. I think they're pretty funny, and also appealing because, while I'm not actually a person who wants to live in an old poorly-plumbed house in an urban neighborhood instead of a giant cheesy suburban McMansion, I wish I were. I have aspirations of gritty urban authenticity.
Math Lesson of the Day
One of the sections of homework that is due Monday has this problem:
Determine whether these points lie on a straight line:
A(2, 4, 2) B(3, 7, -2) C(1, 3, 3)
Now these are points in 3D space, which is why they have three coordinates each. At first, I couldn't think how to solve this problem easily. (In 2D, you could try drawing them and see if they look like a straight line - though that wouldn't be a precise answer - but my 3D drawing isn't good enough and the paper is too flat to see very well whether the points would be on a line.) After a while, I came up with a solution that I'll describe in a bit.
In class last night, the professor brought this up as a homework problem that students typically don't know how to solve, and she told us how to solve it. This official method is much simpler and more elegant than mine, so here is how it works.
If three points are on the same line, then the distance from the first one to the last one (along the line) should be the sum of the two distances inbetween. Here's a diagram I drew:

You can see in the top figure, the points are in the line, so the distance "c" is the same as the sum of a & b. In the bottom figure, the points are not in a line, so "c" is the third side of a triangle, and thus it's a shortcut from a to c, so it's shorter than a + b.
Makes sense, right? Why didn't I think of that?
So here is the overly complex solution I used. I know how to take 2D points and get the equation for the line they would be on - this is something you learn in algebra at some point. (It's possible to get the equation for a 3D line, but I don't know how - apparently we learn this later in the course.) So I reasoned that if the three points are a line in 3D space, they must also be a line in all three of the 2D combinations.
In math terms, what I mean is, given the points above:
A(2, 4, 2) B(3, 7, -2) C(1, 3, 3)
where the first value is the x-coordinate, the second is the y-coordinate, and the third is the z-coordinate, the points should form a line in each two-coordinate system, meaning these points should be on a line:
xy: (2, 4) (3, 7) (1, 3)
yz: (4, 2) (7, -2) (3, 3)
xz: (2, 2) (3, -2) (1, 3)
When my teacher gave the method of solving this in class, I mentioned having used a different method, so over the break, I showed it to her. She had to think a minute before deciding I was right.
The key is that showing the line in each of the 2 dimensions is the same as projecting it onto each plane formed by the axes of the graph. You can imagine a 3D graph if you look at the corner of the room you are in. The corner that goes up and down is the z axis (by the conventions used in this class), the bottom of the wall that goes to the left is the x axis, and the bottom of the wall that goes to the right is the y axis.
So now imagine that in the room, we place three points (just dangling in space), which may or may not be in a line, and we string ropes between them. Of course, if you really did that, you could probably see if the points were in a line or not. But to project them onto each of the three planes (the same as my method of seeing if the three sets of 2D points are on a line), you could shine a light through the points onto each of the two walls and the floor. If the points are in a line, a line shadow will show up on each wall (and the floor). If they're not, you might get a line on one or even two walls, but at least one wall will show an angle (two sides of a triangle) instead.
Once the professor agreed with me about this (not the room analogy, just the "projection onto each plane" thing) I felt very clever, even though the "official" way of solving this problem is much simpler and more elegant.
Wednesday, August 23, 2006
The Joy of Cataloging

My mom (cataloger extraordinaire) emailed me this article about (library) cataloging. Ever wonder how someone could want to have this job? Maybe it's because of this:
"Though most catalogers don’t have the luxury of reading everything that comes across their desks, it’s amazing how much you learn through osmosis while figuring out what a book’s about and how to treat it. I often feel like I get paid to learn every day."
or things like this:
"Oddities we’ve found at my library recently include an OCLC record for a box of Band-Aids, photos of some sort of German festival in which participants dress as haystacks, and a squirrel sewing machine (don’t ask). Not too long ago a friend two cubicles down got to catalog something that appeared to be an
inflatable swimming pool (it turned out to be a globe). Another found an OCLC record for a book that, according a note, was “impregnated with cheesy smell.” My coworkers and I like to talk about “the whimsy of cataloging.”"
Tuesday, August 22, 2006
Back to School, Part 2: Intro to Proofs
Dr. Johnson is in his 60s and really reminds me of my grandfather (my father's father). Of everyone who reads this blog, only my mom[m] has ever met this grandfather, so I guess all I can say is that my professor is also somewhat like Tom Bosley. He's very friendly and funny.
He handed out a syllabus - his own syllabus - and then proceeded to go over it, admitting in the process that three separate things on the syllabus are not true. It is not true that we can't miss more than three classes without penalty ("the only penalty is from you...you're adults, I'm an adult, I'm not going to penalize you for not coming to class"), it is not true that homework can be collected any time ("no, I'll only collect homework if I tell you ahead of time that I'm collecting it"), and it is not true that one of several specific models of graphing calculators is required for the course.
He also gave us the deparmental syllabus for the class. He thinks all professors should do this so you can see if you're getting what you're supposed to be getting. That was interesting.
We briefly talked about some famous mathematicians, then started talking about logic.
The first time I was introduced to formal logic, as far as I can recall, was in a summer enrichment class at Rice when I was in middle school. It was pretty easy for me then. Since that time, the subject has been covered thoroughly for me in at least my high school geometry class and the logic class I took at Rice (in college). So this material - discussing AND and OR, constructing truth tables - was pretty dang boring. It's not difficult enough that you forget it over the years and are refreshed to re-learn it or anything. But it's being presented pretty quickly (probably slightly too quickly if you're not already familiar with it), so hopefully we will move on to something more interesting soon.
We have homework, but he didn't indicate that he'll be collecting it. So given that I don't have the book yet, and assuming the homework is more of this truth table stuff, I don't intend to bother with it.
Back to School, Part 1: Calculus 3
I am not too sure, going into this class, how much trouble I might have with it as a result of basically not remembering a lot of math. (The last time I felt really smart and competent in math was probably my freshman year at Rice - 1992!)
The professor is a woman probably in her 50s with naturally multi-colored hair (some white, some almost blondish, some quite dark) and a somewhat spacey demeanor. But she seems very solid on the math, as you'd expect, and very kind. She started class by taking attendance and making sure each of us passed Calc 2 with at least a C. When I said I took it 14 years ago at Rice ("Where is Rice?"), she was concerned and told me to make sure and come to her right away if I needed help. She encouraged the whole class to come to her for help during her office hours or whenever she is around, and pointed out that the math tutoring lab is a good place to do homework and is right across from her office, so if no tutelage is available there, you can just come over for extra. So she's nice in that way (which most professors seem to be, though a lot don't advertise it as much).
The material in at least this first class was not too hard. It was about graphing things in 3 dimensions. So we talked about the equation for a circle (already known) and derived the equation for a sphere. And drew graphs of things like '1 <= y <= 5' and other stuff in 3D. Then we started the section on vectors. So far, so good. I did run into one math technique I wasn't familiar with ("completing the square") but it didn't seem very difficult.
We already have the list of homework assignments for the entire semester. For each section we cover in the book, there is a set of problems we have to do from the book (e.g., "3, 7, 9, 11, 19"). each problem set is due on the Monday after she finishes covering that section, so if she finishes a section on Monday or Wednesday, the homework is due the following Monday, but if she has only started the section and not finished it, no homework is due yet.
Because I'm crazy and enjoy going back to school, I had stocked my binder with three types of paper - regular lined notebook paper, graph paper, and blank unlined paper. I wasn't sure which would be optimal for the classes. I started taking my Calc 3 notes on the lined paper, but it was making me irritated. When I switched to the blank paper, it made everything so much nicer. So evidently that is the right choice for calculus, which I remembered thinking in 12th grade and at Rice...but it's been a while, you know?
Friday, August 18, 2006
Monday Fatigue
I noticed that when I had tennis classes this summer on Monday nights, I wasn't too tired to go to them. In fact I wasn't really tired on those Mondays at all.
And I just recently remembered that I never used to be tired on Mondays. Coworkers would complain about its being Monday, and I would think, and sometimes say, that I was usually happy and upbeat on Mondays, and didn't mind them. I think my whole life I've basically liked Mondays OK.
So what gives?
I've decided it must be purely psychological. I used to like my job at my last company, despite how screwed up the company was, and when I started this job, I loved it, but lately I've kind of hated my job. So I think the only thing making me tired on Monday is the oppressive thought of having a whole work week ahead of me.
The origin of this Monday Droop is important because, starting next week, I'll have class on Monday night until 8:15. That would be a tiring schedule on any day, but I'd wondered if it would kill me on a Monday. Now that I know that the Monday thing is just in my head, I think I can fight it better. Something that's physical and inevitable seems harder to combat than something that's just an attitude problem.
No more whining and extra fatigue on Mondays! I refuse.
Thursday, August 17, 2006
Translating What?
Translating Thought Leadership... Creating Business Results (TM)
I'm OK with "Creating Business Results", but I have no idea how to parse "Translating Thought Leadership." Is "thought leadership" something they translate? Are they trying to say they are leaders in translating thoughts (in which case "thought translating leadership" might make more sense)? The structure of the whole slogan suggests it's supposed to be parallel, but that only muddies the waters.
Does this make sense to other people?
My Semester
I have two classes, as is typical for the spring & fall semesters for me. I'm taking Calc 3 and Intro to Proofs. Both of them are on Monday & Wednesday nights. Calc 3 is 5:00-6:50, and Proofs is 7:00-8:15 (shorter because it's a 3-hour class).
I'll be coming to work at 8 AM every day. I only take half an hour for lunch most days, so leaving at 4:30 on Mondays & Wednesdays shouldn't be a big deal. The other days, I'll stay until 5.
As school schedules go, this is a pretty easy one. I'll have two hard nights, but the rest of the week is normal. Then of course, I also have my grant project to work on. So it might be a semester with a lot of work. But I think neither of my math classes will have projects or anything like that. Math seems like such a straightforward subject to take classes in.
Then there's the question of whether I'm ready for Calc 3, given that I basically didn't do much calculus this summer at all. (I got through about half of Calc 1 in review before I quit.) Hopefully I can pick up or quickly relearn anything I need to know. I think it will be OK. I'm looking forward to the semester.
My Degree
I gave up on finishing the process last semester because I was running out of time between various projects. I have to finish it this semester, though, because you have to finish a certain number of hours after your plan is approved (21) - presumably to keep you from trying to craft a degree out of exactly the classes you happen to have already taken.
My school (Metro) has minors. So under this program, you can make up your own major (and then have a regular minor), your own minor (with a regular major), or your own extended major. Of course, you have to write up a thing about why your plan makes sense and what kinds of jobs you might look for afterwards, and get departmental approval, and all that.
Anyway, since I wanted to have fewer GIS/Planning/Land Use classes and more Computer Science classes, I called mine "Geographic Software Engineering." I think that sounds pretty cool. It was to be about 1/3 each of GIS, Computer Science, and Math.
Since I've been thinking more about teaching lately, I've been revising this plan to incorporate the types of math classes taken by teachers, and to make sure I end up with enough math classes to qualify for alternative certification in Houston. (It takes 24 hours, with 12 "advanced". In Denver, you have to have 30 hours to be alternatively certified.)
This is my current extended major. Classes in blue are the ones I still need to take.
GEG 1100 - Introduction to Physical Geography
GIS 2250 - Introduction to Geographic Information Systems
GIS 3250 - Computer Cartography
GIS 4840 - Remote Sensing [damn that was a great class!]
GIS 4850 - Advanced Geographic Information Systems
GIS 4870 - Spatial Database Design, Implementation, & Management
MTH 2410 - Calculus II
MTH 2420 - Calculus III
MTH 3100 - Introduction to Proofs
MTH 3110 - Abstract Algebra
MTH 3140 - Linear Algebra
MTH 3650 - Foundations of Geometry
CSI 1050 - Computer Science 1
CSI 2050 - Computer Science 2
CSI 3050 - Computer Science 3
CSI 3210 - Principles of Programming Languages
CSI 4250 - Software Engineering Principles
CSI 4260 - Software Eingineering Practices
This is 62 hours, of which 41 are upper-division. I'ts a pretty strong degree, I think (for an undergrad degree from a mediocre school, I mean) - I'm only required to have 27 upper-division hours. It gets me enough math for HISD, and the math I'm taking is a subset of what teachers here take, so it should look like about the right kind of stuff (that is, more theoretical math and not too much engineering/practical type math).
I have 29 hours left to take, which is basically 2 years for me. Argh. I seem perpetually 2 years away from graduation.
Tuesday, August 15, 2006
Toothpaste for Dinner
Friday, August 11, 2006
Dreams
I've always wanted to teach, but back when I was poorer, I was nowhere near having a degree, and once I got near to having a degree (like, in the past few years), I was making too much money to readily consider taking that kind of cut in pay.
But recently, I've worked out that if all of my debts were paid off (which will take either a few years of disciplined effort, or my company's stock price going up by about $1), I could live on a teacher's salary. And when I graduate, I'll have enough math credits to be a secondary (jr or senior high) math teacher.
I won't have a teaching certificate, but both Denver and Houston have alternative certification programs that involve teaching while going to school for one year (Houston) or two (Denver). The pay is not horrendous - in Houston, I'd make about $30K the first year, which includes a deduction for the program costs. In a couple of years I'd be making $35K, and it goes up from there. With a paid-off car, no other debts, and a slightly cheaper lifestyle than I have now, I could live on that pretty well.
The reason I'd like to do this in Houston is that, given that almost everyone I know lives in Houston or Austin, it kind of sucks to live in Denver, even though Denver itself is fabulous and, if I had my druthers, everyone I love would move here instead. If I got my certificate and taught a couple of years in Houston, I could try to get a job in Austin later if I wanted to. Colorado and Texas are also reciprocal with regard to teaching licensure, so I could also move back to Denver if I chose. (Conversely, I could get certified here and then move to Texas.)
What I really don't know is whether I would actually detest and loathe teaching. In theory, it really sounds great to me. But in practice, it seems like a lot of people really hate it and want out. Would I be one of them? It's not as though it would ruin my life if so. I can come back and get another job in oil & gas or GIS, or try to start a new career in computer science - especially if I've successfully adapted to living on $35K or so.
Lately I'm trying to think of money not in terms of something you want to stockpile so you can live bigger and better, but in terms of something you want to cut your dependency on so that you can make your life about other things than having to maintain a certain income level. It's not retirement that I'm after (though being independently wealthy is always welcome, and of course I do plan to retire someday and not have to live on the street) so much as a life that is more fulfilling or more enjoyable or more involved than what I currently have.
Friday, August 04, 2006
Tam Rules the School: CREU Grant
So we submitted a proposal. My partner Olga was interested in diabetes research (she was an endocrinologist in Russia), so we put together a research project about creating some type of a patient database to be used by different doctors remotely that would then use some type of artificial intelligence algorithm(s) to recommend treatments based on similar cases.
Well, it's been about a month since I thought we would be notified, but we finally found out that we got it! Yay!
At the time that we applied, the grant amount was supposed to be $1500 per student, but since then it has changed to $3000 per student, so that's extra exciting. We apparently were also awarded $500 for conference travel or other related project costs. (The money is exciting, partly because we had already decided to work on the project next year anyway, for general experience, resume building, and possible independent study credits. So it was a question of "work hard on something all year for intangibles" or "work hard on something all year and get money.")
We are required to keep a weekly journal of our efforts and an updated web site about our project. The three of us are (tentatively) going to meet the week after next to get started.
Edited to add this note: a semester of school costs me about $1000, so this is, in essence, a full scholarship for this upcoming year for me.
Wednesday, August 02, 2006
Thrive
This ("Signs") was my first favorite one. I especially love the Hal Hartley-esque music:
I also think "Be Your Own Cause" is brilliant, both in the message and in the solid boomer targeting. The Dylan music is great too.
Here is a nifty Spanish one:
And here is one I haven't seen on TV, but it looks great too:
I just think the message of these ads is fabulous, and they are so well-executed. Unbelievable :-)
 (from
(from 



















