The Extended Euclidean Plane

Here is a little bit of fun geometry that isn't too hard to understand (I promise).

As you probably remember or can easily confirm, in regular (Euclidean) geometry, any two points determine a unique line (that is, there is exactly one line that goes through both). And two lines either cross each other one time (that is, they have one point in common), or they are parallel and never meet.

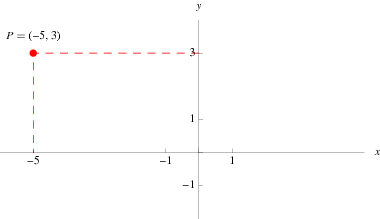When we talk about "the Euclidean plane" (which is just the usual flat space used in normal geometry), one way to define it is this:

• A point has two coordinates (x, y), each of which is a real number (as shown on the right).
• A line has the form ax + by + c = 0 for some real number values of a, b, and c. For instance, defining a line as "y = 2x + 4" is the same as saying "2x - 1y + 4 = 0".
• A point is on a line (and the line contains the point) when the point's x and y coordinates satisfy the equation for the line. For instance, the point (1, 6) is on my example line above because 2(1) - 1(6) + 4 = 0.

In the geometry course I'm taking, the definition of a particular geometry follows this pattern: you define what the points and lines are, and how they intersect.

What we talked about last night is the extended Euclidean plane, which exists in order to get rid of the annoying concept of parallel lines. (They're "annoying" because they muddy up some theorems, which I won't get into.) The extended Euclidean plane is different from the normal Euclidean plane in that any two lines that are parallel in the Euclidean plane are said to meet at a "point at infinity." Every class of parallel lines (that is, any set of lines that are all parallel to each other, or all of the lines with the same slope) has a unique point at infinity at which all of the lines meet. And all of the different points at infinity make up the "line at infinity." Well, why not?

So, the extended Euclidean plane could be described like this:

• The points include all points of the Euclidean plane, plus a point at infinity corresponding to each class of parallel lines (alternately, corresponding to every slope).
• The lines include all lines of the Euclidean plane, plus the line at infinity.
• Euclidean lines contain all of the points they would in the Euclidean plane, plus the point at infinity corresponding to their parallel class. The line at infinity contains all of the points at infinity.

This leads to at least one nifty result. Now, in addition to this:

• Any two points determine a unique line.

we also get this:

• Any two lines meet at a unique point.

These statements are "duals" - formed by changing points to lines and collinearity (being on the same line) to concurrence (meeting at a point).

Fun stuff!