A Strange Success

Ed and I have always had a hard time keeping the kitchen clean. That is an understatement, really - at any given moment our kitchen was very likely to be completely overrun with enough dishes to fill the dishwasher several times over. Periodically we would beat back these hordes by doing a bunch of loads, but it always regressed to the same state. We tried various ways to fix this, to no avail.

About six weeks ago, I told Ed that this was really bothering me. I need to be able to make food at home and the way we were keeping the place wasn't conducive to that. I suggested a new regime.

The suggestion was actually really simple - I proposed a rule that no dishes could be put on the counter. Dirty dishes must go in the dishwasher. If the dishwasher is full, it should be run; if clean, it should be emptied. Half of the sink is reserved as a space to work in, but the other half is available for dishes used while the dishwasher is actually running.

Ed agreed on the condition that we also have a rule of no trash outside of the garbage pail, including in the living room. Fair enough.

There was one additional touch. In the past, because we are both (in some ways) slobs, and both stressed and bad at taking care of things, we've cut each other a lot of slack on things like this. But I stressed that this time around, if one of us wanted to be nice to the other, this could only be done by taking care of the chore the other person couldn't do, and not by letting it go. In other words, if I've left some dishes on the counter and Ed wants to be nice about it, the proper way to do so is to put them in the dishwasher for me - not to just let me off the hook.

It was pretty obvious that this new regime, merely consisting as it did of a new rule - and, what's more, a new rule that was already obvious and should have been the guiding principle already - would not work. And yet it has worked. We've had a clean kitchen ever since.

Weird.

Some Thoughts on Math Education

I've been reading this article, "A Brief History of American K-12 Mathematics Education in the 20th Century" by David Klein, and I wanted to write some of my own (basically uninformed) thoughts on math education.

As in some other academic areas, there is a sort of conflict in math education between the rigorous teaching (through repeated practice, drilling, etc.) of basic math skills and a more learner-centered, discovery-driven style of teaching, where students are encouraged to think critically and find their own paths forward, often by inventing their own ways of doing math or by solving novel, difficult problems.

Obviously this is not an either/or proposition, and unfortunately no style of math teaching is known to result in a uniformly well-educated population. I am ignorant of actual empirical findings in this area (and in any case skeptical of many of the types of empirical findings that I suspect exist, on methodological grounds), so I do acknowledge that everything I'm saying is essentially just based on my opinions from introspection and observation of the world around me.

In order to be any good at math, in order to solve new (to you) types of problems, and so on, you do need to practice the skill of working on an unknown new problem which isn't susceptible to a specified set of skills (as opposed to most of the exercises at the end of the section of any math text, which are usually basic applications of the techniques taught in the section). I think that this type of work is also what math is, on some level, about, and that discovery-centered learning (or whatever it's called) can lead to a great appreciation of math as a field.

On the other hand, if you can't reliably add fractions (as many of my precal students cannot), your ability to explore new problems will be severely constrained. If you never learned long division because your teachers think it is boring and obsolete in the age of ubiquitous computing devices, you'll find it harder to learn polynomial long division, and when you encounter a more novel problem later, you may not even imagine it as a way forward. If your notion of a limit is only vague, you won't be able to write an analysis-style proof to solve a problem in a metrizable topological space. If you can't compute a double integral you may never understand the unique properties of the normal curve. If you can't mechnically process the symbolic logic behind a proof by contradiction, you may introduce logical errors even when you understand the argument you're trying to make.

All of which is to say that doing anything interesting at a given level usually relies on the boring techniques of previous levels.

I had a funny moment the other day when I needed to compute some zeroes of a function for my own work, because I realized I was using an exact skill I had just taught in our precal class. I think my precal students probably imagine that my work is a lot more like theirs than it actually is (almost none of my work involves computational "problems"), yet here was an elementary technique from their class which I absolutely needed to use in order to proceed.

Returning to my uninformed ramblings about younger students, there is also this. Little kids should not be bored into submission by having to do pages and pages of long division problems while being forbidden from exploring their own math interests (or discouraged from ever having those interests). At the same time, some kids (and adults) enjoy the part of math where you learn to do something neatly and properly and then execute that skill over and over. (I enjoy this aspect of proof-writing, so this enjoyment can also exist on a level well past arithmetic.) That enjoyment is not wrong or somehow antithetical to the spirit of mathematics, and the frustrations a kid may feel with never being taught a correct algorithm for doing anything and being expected to derive and explain her own methods for every new thing are also legitimate. (On a practical level, a ton of jobs are ideally suited to people who enjoy being methodical and careful, and cultivating that habit is a proper function of education.)

In my ideal world, people would have some appreciation for the abstract qualities of math, and at the same time, would feel comfortable doing the kinds of manipulations they find helpful. They'd be able to double a recipe either by using reasoning to develop an ad hoc method or by relying on a trusty algorithm for fraction multiplication. Would-be engineers would show up to college with at least the basic skills required to study calculus, and kids predisposed to be mathematicians would arrive with some experience having fun working on hard or weird problems.

Bad Week

I usually post cheerful things, but not today. I'm not sure whether to organize this post by subject or by calendar, but let me start by subject.

Topology

We had an in-class midterm Thursday morning. I left 3 out of the 5 questions completely blank. This exam also has a take-home portion, originally due Tuesday but now technically due Thursday. I have answered three of the questions so far and I have worked several hours on each of the other two questions with no results.

One of those two was originally wrong, which I pointed out to our professor (gingerly, since I am usually mistaken about such things), and so he fixed it (hence the new due date). The new question is similar to a question we had in our last homework which I couldn't answer then, either. I can get 10 bonus points for turning in a counterexample to the original statement, which I have written up.

So basically I am up to 60/100 points for this exam, and the maximum I can get (considering the lost points from the in-class part) is 80/100. I have no reason to believe that low scores are OK in this class and I think most people will be able to get the problems I couldn't get.

Algebra

We had an in-class exam Friday afternoon. I wrote correct (I believe) answers for 2.5 out of 5 problems, and a woefully incomplete answer for 1/2 of another problem. I'm expecting around a 50% on this exam. We also have an assignment due Thursday which I haven't even looked at.

Probability

I would have had a meeting with my professor for this reading course on Thursday, but I asked him to postpone it, so we meet tomorrow morning instead. I have four assigned problems this week, of which I have completed 1.5. There is another question that I can tell is extremely easy but I can't find the math to express the question and so I can't possibly give an answer. I haven't even looked at the fourth question.

Normally we would meet again on Thursday by which time I would have read another section of our book and answered the questions for that section, but I can't see that happening at all. I have no idea how much of this the professor will tolerate; he doesn't have a particularly tolerant demeanor.

So basically I feel completely doomed right now. Everything I work on turns to shit. I should note that, unlike in most of my life so far, I am not in this position as a result of slacking off. I've been working hard the entire semester. I studied for both exams and felt reasonably well-prepared for each one. I've taken about three Sundays off this entire semester.

Anyway, that's my life at the moment.

Thoughts on Teaching

This is my second semester teaching precal recitations (what some schools call "labs"). The kids in my course attend a large lecture with their professor three days of the week, and the other two days, they have recitations, which are 50 minutes long and in small classrooms (about 35 students).

It is an interesting experience. Every Thursday I give them a quiz or an exam given to me by the professor, and on Tuesdays, and Thursdays before the quiz, I go over material with them, answering their homework questions and reviewing stuff for the upcoming quiz or exam.

Teaching (the actual teaching part) is really fun, but also weird and frustrating. When I gaze out at my class, many of them look either terminally confused or completely bored, and I can't always tell which. Many of my students totally ace all of the quizzes and exams - they probably don't need me for that. Some of my students struggle around the middle, and hopefully I help them. And some of my students are just consistently confused and their quiz answers are weird and wrong.

One thing that happens is that I don't know how to pitch my class. I know some of my students really aren't getting certain things - do I just hammer on things endlessly, trying to bring everyone along, while boring the others out of their skulls? Or do I sort of blithely move on to the newer, more exciting material, risking leaving some in the dust? There isn't one answer to this question - it is more of a feel thing, and I don't think I have the feel of it yet.

Another thing I find myself doing, and what I really want to talk about, is focusing on mistakes. There are certain persistent mistakes made by my students that sort of drive me nuts. For example, a lot of my students think (at least while taking a quiz) that the square root of (x^2 + 9) is x + 3. Or (the same error) that (x+y)^2 = x^2 + y^2. Or they add or multiply fractions completely wrong.

These are really basic mistakes that they should know better than to make, and it's easy for me to sort of become obsessed with these errors and how I can drive them out. And I'm realizing that focus is completely wrong.

I've had professors who seem more focused on mistakes than on the math they are teaching, and it's made certain classes very negative for me. It starts to feel like the point of the class is to avoid errors, to not fall into certain common traps, and so on, rather than to learn exciting new math. What's the fun of that?

I've also seen professors focus too much (I think) on their fears about students not being prepared for the next course. I don't know if this is universal, but I had a lot of middle school teachers who would say things like, "I can't let you get away with xyz, because your high school teachers will never allow that," and high school teachers who said the same thing about college professors. It never turned out to be true. And I've seen profs at my school wield calculus in the same way - "If you can't do [this particular skill], you will fail at calculus."

It's not that it's false. Your lack of ability to add fractions will increasingly be a handicap as you proceed through the calculus sequence. But I'm not sure threatening people with the upcoming courses is really the way to go. Some level of mistake-making is normal, natural, and not indicative of future failure. People get better all the time, even when they are making mistakes.

Some of them really will go on to fail calculus. Some will fail precal and not even get to calculus quite yet. But making calculus sound dire and horrible to everyone won't necessarily solve that. Calculus is one of the most beautiful inventions of the human mind. Being able to study it is a great luxury. They should look forward to it!

So despite my controlling tendencies I am going to make an effort to keep a positive focus in my teaching and not become obsessed with typical student errors and mistakes. I really don't want to be that kind of teacher.

Socialization

I have experienced an interesting attitude change since starting grad school.

Ed (my ex-boyfriend, with whom I still share an apartment) and I are in grad school together, as most readers of this blog know. Before coming here, we'd had one class together at my undergrad institution, and that was when I learned that we have similar classroom styles (as students), except that his style is more extreme. We both tend to ask more questions (and answer more questions posed by the professor) than other students, and are prone to...well, sort of acting as though we are the only student in the room and can just freely interact with the prof without regard to what s/he is trying to accomplish with the class.

In the math pedagogy class that I took, our professor once gave us a list of problem student types, one of which he called "Mr. Non-Sequitur," giving the example of that guy who always asks you how such-and-such relates to fractals. At the time, this reminded me of Ed, who will often ask tangentially related questions.

Last year, I found Ed's classroom behavior pretty obnoxious, and worried that mine was obnoxious as well. But then this year, I observed that, in talks, many of the professors in our department behave exactly the same way. Whether the speaker is internal or external, they will interrupt with questions, make nitpicky corrections, and ask about strange tangents. And, though there is no way to put this on my public blog without risk, I will say that the professors who act this way are some of the ones I respect the most (independent of their behavior in talks). This is also the talk-watching style of the genius among the grad students of our department.

Maybe this is normal, socially appropriate behavior for my discipline.

I was curious what would happen when Ed took another class with our pedagogy professor, who is a bit strict in his classroom management style. Would he quash Ed's interrupting tendencies? The answer turned out to be a pretty big no. If anything, I think he appreciates being interrupted, nitpicked, and asked weird questions. He told me once that we were his best class in many years because we are so engaged and challenging, and I think he also gave private positive feedback to Ed once.

So I have basically totally revised my opinion of this style of behavior, and now think it must, indeed, be socially appropriate in our field. This led to an interesting conundrum recently, however, when one of my cohort gave a talk.

The talk was very interesting. At one point, though, Ed stopped the speaker to ask, basically, "So what?" He didn't use those words but wanted to know about the motivation for something she was talking about. She didn't have an answer right away, and he said, "I just think I would get more out of this if I knew why we were talking about it."

I felt like it was a bit over the top, given that she is our friend, is a bit early in her career (like we are), and may not have been completely confident in giving the talk. I wouldn't have pushed her in that way myself.

Now, I think Ed just asked the question because it was on his mind. But I wonder...maybe it is our job to socialize each other by asking these kinds of tough questions, even if it makes the speaker uncomfortable. You could argue that we should refrain so that our friends can be more comfortable, or that we should intentionally not refrain so that they can toughen up and not be stymied in (e.g.) a job talk later, when someone in the audience is of this more obnoxious cast.

Fortunately, our department has a good mix of people who like to speak up and people who don't, so I guess it will all just average out. But these are just some thoughts I've been having lately.

Teacher Follies

An amusing/embarrassing thing happened to me today.

Because I write so much, I am very careful to keep paper that I've only used one side of to use as scratch paper. I have a big stack of this on my desk, and when students come to see me, I usually write with/for them on some of this paper, and then if they want, I let them take the paper with them. I figure the graduate math on the other side won't hurt them any (though it hurts me plenty, I can tell you).

Anyway, sometimes when I am working on problems, I write notes to myself in the margins. Often the notes say something like, "I suck at this type of problem :(" or "I will never get this!!!!" I try not to give papers like that to students, but I don't try very hard.

Yesterday, a guy came to my office hours and I sent him away with three sheets of my scratch paper. Today before class, he was showing it to another student, and I overheard this conversation:

Other student: Huh. It says "I am a bad ass" on this side. Did you [to the first student] write this?
First student: No, I think she wrote that. This is her work for some other stuff.

So I wandered over and sure enough, I had written "I am a bad ass" in the margin of my work. We had a good laugh over it.

It's kind of embarrassing, but I'm glad it was positive self-talk for once, and not the negative kind. One of my friends in the program pointed out that it was good that I had at least not written that I was a BAMF, which is also something I might write (either as an abbreviation or written out).

So anyway, there's that.

Measure-Theoretic Probability

This is definitely my hardest semester of grad school so far, for the simple reason that I am taking two core courses (which are the kind here that require the most work) plus a reading course in measure-theoretic probability, which is taking as much time and effort as a core course (and more than either of mine, actually). But I'm increasingly wanting to go in a probability direction with my studies, so I'm thrilled to be doing it, and I'm really enjoying it so far.

The core course I took last year was in measure theory. I've written about it a little before, but today I'm going to (briefly) explain its relationship to probability. Then I'll end the post with my real reason for posting, which is a quote that excited me this morning.

Measure is just (more or less) a generalization of length. Let's say you're on the real line and you want to know how big a set is. If the set is just an interval, like (0,2), it's easy enough to say its length (or measure) is 2. But what if your set is much weirder? Like, what if you want to be able to say what "size" any subset of the reals is, in a sensible way that accords with our notion of length? That is, you'd like the interval from 0 to 2 to still have length 2, but you still want to be able to measure anything you want?

Well, unfortunately that is impossible, but what we can do is come up with a measure that works for pretty much any set that anyone cares about. In fact, coming up with a set that you can't measure requires using the axiom of choice to construct some bizarro thing that just doesn't arise in normal life.

So, let me tie this to probability. Let's say you want to pick a random number between 0 and 1, with all numbers equally likely. I'm just talking about a uniform distribution on the interval [0,1]. It's pretty obvious (I think) that the odds of getting a number between 0 and 1/2 is 50%. This corresponds to the length of the interval that you're talking about.

But what about the odds of getting a rational number? Or the odds of getting a number without a 2 in it anywhere? Or the odds of getting a number whose first three digits (after the decimal point) are repeated 9 times?

These are questions which can be answered with measure theory. In particular, there is only one measure (it's called Lebesgue measure) which both assigns to each interval its length and gives a measure for every Borel set (the ones I'm characterizing as "all the sets anyone cares about").

You might ask, "Who cares about the odds of getting a number whose first three digits are repeated 9 times?" But let's unpack that a little bit.

Let's say we roll a 10-sided die an infinite number of times. If the sides of the die are labeled 0 through 9, then if you wrote out the results, after a decimal point, you'd get a number in the interval [0,1]. For instance, it might look like .98362819501... and so on.

If we assume all combinations of die rolls are equally likely (which is true if the die is fair), then the odds of the die roll meeting whatever criteria we give are exactly the measure of the set in [0,1] that corresponds to the numbers that the roll represents.

For instance, let's look at my question about rational numbers. I should note that we're not going to let anything terminate, so for instance, we wouldn't write 0.4 (because that wouldn't correspond in any obvious way to an infinite series of dice rolls) - we would write 0.399999999..., which is the same number.

So what is a rational number? It's one that repeats forever when you write it out like that. For instance, 1/3 is 0.33333333.... You could also have a rational number like .123123123123... where more than one number repeats.

So, if we randomly choose a number between 0 and 1, the odds of it being rational are identical to the odds that, if we roll a die infinitely many times, eventually we hit some number or group of numbers that then repeat forever (for instance, we start rolling 1,2,3 over and over again for all eternity). Common notions of probability suggest that the probability of that happening is basically nil, which turns out to be right - the measure of the rational numbers is 0. (This is proved in an entirely different way in a measure theory course.)

Or, to use my other example, the odds of having your first three rolled numbers happen again like that 8 more times in a row is the same as the measure of the set I mentioned earlier - numbers with their first 3 digits repeated nine times. (So in other words, you can use this to measure probabilities that happen in a finite number of dice rolls too.)

This leads me to my quote, which is from Section 4 of my textbook, Billingsley:

Complex probability ideas can be made clear by the systematic use of measure theory, and probabilistic ideas of extramathematical origin, such as independence, can illuminate problems of purely mathematical interest. It is to this reciprocal exchange that measure-theoretic probability owes much of its interest.

So there you have it. Nifty, no?

Two Easy Recipes, and a Bonus Low-Rent Dessert!

I basically only cook things that are extremely easy, so here are two simple recipes, plus a bonus dessert.

Chicken and Rice Soup

1 package chicken thighs (bone-in)

1 cup rice

1 bag frozen mirepoix (diced carrots, celery, and onions)

1 tsp salt

Put chicken thighs, salt, and mirepoix into a pot and cover with plenty of water. Boil until thighs are cooked (about half an hour). Remove thighs. Remove and discard skin, and separate meat from bones. Return meat and bones back to the pot and simmer another half hour or so. Then remove the bones and add about a cup of rice. (Confirm by eye that there is at least 2 cups of liquid in the pot; more if you want genuine soup rather than, as I prefer, something more like chicken and rice.) Simmer for another 20 minutes.

Beef Stew

1 package (1-2 lbs) stew meat

1-lb bag baby carrots

2 or 3 large potatoes

2 cups beef broth

1 cup wine (optional)

1/2 tsp salt

pepper if desired

Cut up potatoes (peel first if desired) and place all items into a large pot. Simmer gently until cooked, about 2 hours, or cook all day in a crock pot on low.

Low-Rent Banana and Chocolate Dessert

1 banana

part of a chocolate bar (I use 2 squares of a Lindt 85% cocoa bar, but any chocolate bar should work)

plain yogurt (I prefer whole milk)

Cut up the banana into a bowl. Break the chocolate into small pieces and microwave for 30 seconds at a time in a tiny bowl until melted. Gently spoon/pour the chocolate on top of the banana pieces. Glop a bunch of plain yogurt on top. Enjoy!

Reading Course FTW!

This semester, I am doing a reading course in probability & measure (using Billingsley). It's the first time I've ever done a reading course or any kind of independent study (other than my grant, but that was very different).

This was the first week of school, so last week I emailed the professor to ask when he'd like to meet or whatever, and we set a meeting for today. He gave me a section to read and some exercises to look at.

I've spent probably literally (not counting Internet-procrasting-time) 20 hours on that section and the exercises this week. The book is very dense for me and the exercises were difficult. I ended up with 10 typed pages of answers. I wasn't sure if he would want me to turn those in or just discuss them or say that I had done them or what.

So we met today. The scoop is that, whatever questions we don't discuss to his satisfaction in our meetings, he will have me turn in (I ended up turning in the whole set since I had it all stapled together, though we talked about most of the questions). The meeting went well - I was comfortable presenting answers on the board and discussing the material. He told me how to do the problem I hadn't managed to figure out, and the answer was really cool (really cool).

I've been exhausted all day. The first week of school is rough and I've been working hard. I'm the kind of tired where my head naturally goes slanty and I become slack-jawed. I'm the kind of tired where I think I must look really tired even from the outside.

But that meeting was so energizing, and I think this course is going to be great. I'm realizing that, actually, I think reading courses are super fun, way better than classes. Instead of sitting in class for 3 hours a week (which I hate even when it is informative), you get to work on your own with a book (which I love even when it is really hard). It's fun in the way that my summer of qual studying was fun.

Guess what? Reading and figuring out math on your own is more fun than a class. That's a really cheerful thought for me.

I'm still worried about my workload this semester. I have two core courses plus this reading course. But I feel motivated towards at least one of my courses, and of course towards the reading course, so I'm feeling pretty good right now. And I'm looking forward to doing more reading courses in the future, bigtime.

Silas Marner

I just finished reading my second George Eliot book, Silas Marner. I chose it to read because I wanted to read another book by her and I had heard of it. I got it for free (in Kindle form) from Amazon.

The basic idea of the book is that a man named Silas Marner has lost his faith after being (in essence) exiled from his (what we would now call) fundamentalist religious community, and has settled in a new town, where he becomes a miser and a recluse. Then a series of strange events involving a nobleman and an unwanted child alter the course of his life.

Before I read it, I read a review on Amazon, by a Susan Hallander, which begins thusly:

Question: How can you ensure that a person will hate a book? Answer: Make her read it for 7th grade English class, make sure that the language is old-fashioned, and above all, make sure that the ideas and concepts are over her head. If that's what happened to you, and that's why you have an aversion to Silas Marner, and you are now over 30, pick it up again. Read it twice. Silas Marner is one of the greatest novels in the English language.

As a result, while I was reading it, I had that context in the back of my mind - what would it have been like to read this in 7th grade?

Ultimately, while I enjoyed reading it, and was always reasonably eager to continue, I found Silas Marner disappointing. In some ways I would have enjoyed it less in 7th grade, but in other ways, 7th grade might have been a better time to read it. I probably would have appreciated its folksy moralism better when I was younger and less cynical.

I don't know what to say about this book in terms of anyone's decision of whether to read it or not. The book it most reminded me of, that I did read in school, was The Scarlet Letter, but that's probably a rather ignorant comparison.

My Changing Musical Preferences

I was emailing with Sally today about the increasing distaste I feel for the habit of rating everything one encounters, and it occurred to me that this relates a bit to my changing tastes (or, really, a change in the way that I have tastes at all) in music.

When I was a kid (through middle school or a bit beyond), I liked most of the music I heard, though of course I liked some things more than others. But I was largely unconscious of what I liked - I usually didn't know what bands or artists or albums the songs I liked came from (with the exception of the music my mom really liked, which she would tell me about). I just listened to the radio and liked what I heard and was crazy about a few things. (Some songs I remember being crazy about: Do Ya Think I'm Sexy? by Rod Stewart, Strip by Adam Ant, We Built This City by Jefferson Starship.)

Sometime in high school, I started to really have taste. There was some music I loved (Erasure, Depeche Mode, Midnight Oil, Jane's Addiction, The Cure, plenty of other stuff I'm not thinking of at this moment) and other music I loathed and detested (New Kids on the Block, Tiffany, Madonna - who I had loved when I was younger - and in general most top 40 things). Through college and beyond, I developed and expanded and refined these tastes, and they were a part of my identity. (This identity-by-tastes seems really common among my friends, particularly younger ones.)

When I was 19, I think, I did have a surprising experience. I hated the song "Vogue" by Madonna. I was visiting the Netherlands at the time, and I walked into a club with some friends. In the club was a leather-clad half-naked guy in a cage, and he was dancing to "Vogue." And it was the perfect music for exactly what was happening in that moment. I had not known such a phenomenon could occur: that a song you hated could turn out to be perfect for a particular occasion.

I've noticed over the years since college that my musical tastes are not only expanding but in general just loosening. There began to be a ton of music that I enjoyed hearing despite not officially "liking." (For instance, I am now ready to admit that I really do love hearing the song "Dust in the Wind." I will always sing along.) Sometimes I felt as though, if my friends learned of my real tastes, they'd think less of me.

That kind of anxiety is part of why we (some of us, anyway) identify with the famous xkcd cartoon about Pandora:

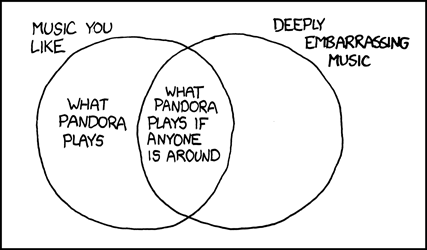It seems silly that there is such a thing as "embarrassing music" in a way. People make all this music for us to listen to and enjoy - what is embarrassing about enjoying it? I mean, I'm embarrassed about liking "Dust in the Wind" which is not exactly nazi death metal or anything. It's pretty innocuous.

I am moving more and more towards viewing my musical tastes as being more probabilistic (I tend to enjoy dance music, alternative, 80's pop, blue grass, dixieland jazz, and Beethoven, and don't tend to enjoy metal, classic rock, new country, or jazz, but I can enjoy a lot of things in the right context) and not really related to my identity. It's actually hard for me to let go of the idea that musical tastes have more than practical importance.

But I am getting more and more to the point where it seems useless to describe various artists as good or bad. Sally and I both remember a time that Robin defended Pearl Jam (who Sally didn't like) as "a quality product," but most commercially produced music could be so described (depending on what qualities you think are important). Does Garth Brooks suck just because I don't really like his sound and his lyrics aren't clever and edgy or deeply meaningful (for me)? Or is he great because his music (apparently) brings pleasure to millions of people? Who cares what I think anyway?

Where My Money Goes

Unlike in my former life as a corporate worker bee, these days I spend more money than I earn. Not counting the tax hit from the bonus I got when I left my last company (which, after all, came with a bonus), I'm about $2000 poorer (in terms of cash and short-term savings) now than I was a year ago.

I'm not too upset about that. I started grad school with some savings that I expect to partly deplete by the time I graduate. At the same time, considering that I live in a relatively cheap apartment ($675/month) with a roommate (so that my rent + utilities is typically under $400), my TA stipend (about $22,000 a year including the extra summer work) really ought to be enough to live on. Many people are supporting families on such a wage.

I keep track of my finances in Mint, so for your amusement and/or horror, let's take a look at how I spent my money in 2011. First, here is an overview of all of my spending:

A few things really stand out:

1. Wow, I spend a lot of money on food!
2. And shopping!
3. What am I spending all that "Auto & Transport" money on?
4. I wonder what is in "Other"?

(In case you wonder, the Education spending includes $5 of tuition and the rest is books and office supplies. Some of the books are textbooks and others are supplemental reading. I also spent $180 on eBay for the tablet I teach from.)

Let's look at where my food budget goes:

So, it turns out that I eat out a lot. This shouldn't surprise anyone who knows me. And this aspect of my life has proven extremely unresponsive to my attempts to apply budgets to it. It turns out (via the magic of revealed preferences) that eating out, and in general having nice things to eat, is important to me. I'd still very much like to spend less money on food. Over $20 a day seems a bit excessive.

Now, about the shopping:

I'll admit it shocks me that I spent over $1000 on clothes in 2011. I don't think of myself as buying many clothes (even including shoes, which are included here). I'm fine with the money I spent on books. The 'hobbies' money here was the money I spent having the photo albums of my childhood digitally scanned and I don't regret that either.

Now let's take a look at where my "auto & transport" spending is coming from:

The parking is mostly for school, of course. I shouldn't need to spend money on this at all given that I live half a mile from campus, but I started buying parking because I developed chronic foot problems that seem best remediated by avoiding walking. Hopefully over time I can cut that expense. The rest of this is just the normal costs of car ownership.

Let's take a look at "Other":

I'm happy with the money I spend on travel - I think it's money well-spent, relatively speaking. Visiting my loved ones is important to me, and if anything, I wish I spent more money on this. (That is to say, I wish I traveled more. If I could travel more for the same money that would be great too.)

What about that $418 on entertainment?

You might think from seeing this that I buy movies, but that is not the case: if you look at the individual records, it turns out that a few of these are movie rentals and the rest are actual theater tickets. (There is also my Netflix subscription for $10/month.) I hardly ever used to go to the movies, so it's a bit shocking that I apparently saw 25 in the theater this year.

Seeing movies in the theater is a bit of an extravagance, but it results from the social life I have these days that I never used to have. I really relish that aspect of my current existence and don't regret it in the slightest. I will continue to see movies with friends as much as I want.

So that's how I spent my money in 2011. I would like to cut back on shopping and on eating out; otherwise I'm relatively satisfied with my current choices, and very grateful that my life affords me so many opportunities.

Middlemarch, and Being Human

A long time ago at a college far, far away (well, about 6 hours away by car), I was supposed to read Middlemarch by George Eliot for a 19th Century British Literature class. I ended up dropping the class and never reading the book, but then recently, Ta-Nehisi Coates has been talking it up, and I love him, so I was inspired to pick it up. I haven't finished the book yet - I've been reading it several hours a day for over a week, but it's a long book - but I want to talk about it a bit.

Middlemarch at first reminded me of Jane Austen's novels - the setting appears similar (Eliot was born around the time Austen died, but from this distance in time, it feels the same) and the book has a large and interwoven cast of characters and is heavily about courtship and marriage. There are three really clear differences, though:

1. Eliot is much harder to read than Austen; the sentences are longer, use more fancy vocabulary words, and are structured with more complexity.
2. If you read Austen novels and think, "But what about once they are married? These people barely know each other! Marriage is every day for years and years and years! Also women especially had no options and they didn't even have divorce back then," Middlemarch may be for you, because getting married is just the start of each story, and you get to find out exactly how the matches turn out.
3. Eliot doesn't limit herself to describing conversations between women or between women and men; she also describes conversations that solely involve men.

There are other differences, one of which relates to an obsession of mine. The obession is the one I'm thinking of when I say, "I don't know how to be a human being," so let me digress for a moment.

Life to me seems like a constant struggle between being a decent human and being a shitbag, and we have two choices - unabashed shitbaggery, or shitbaggery accompanied by struggle and abashedness. I don't see any cure for it, and this, to me, is almost the sole appeal of Christianity - that it starts with a frank admission that we are basically horrible.

Pondering one's own "stuff" gets into what I call fractal territory, which is to say, it leads to an endless descending cycle of realizing what a crappy excuse for a person one is, at the end of which cycle I usually declare, "I have no idea how to be a human being."

I'm not talking about temptations like lying or theft, but actual internal attitudes. I'm talking about things like mocking people we don't like for qualities we readily accept in our friends, or detesting others for traits we ourselves possess, or continually (despite any efforts to the contrary) seeing the world as revolving around ourselves, or constant unremitting disregard for sometimes even really obvious things about the experiences of the people around us, or the bizarre selfish pride most of us feel.

So I guess what I'm really talking about is fundamental selfishness. Of course, some people simply embrace their own selfishness - either by conveniently not noticing it or by taking up a philosophy that justifies it. I know some people who actually seem not to be shitbags at heart, but I have no idea how they attained this state, or whether it's basically illusory. But I know that when I look at myself in terms of my internal states I basically disapprove of my overall implicit attitudes.

And the thing about Middlemarch is that George Eliot seems to really get this. She writes about this sort of thing a lot, and I like it.

Here are some good quotes (not all relating to this topic):

For my part, I have some fellow-feeling with Dr. Sprague: one's self-satisfaction is an untaxed kind of property which it is very unpleasant to find depreciated.

***

We are angered even by the full acceptance of our humiliating confessions - how much more by hearing in hard distinct syllables from the lips of a near observer, those confused murmurs which we try to call morbid, and strive against as if they were the oncoming of numbness!

***

There are answers which, in turning away wrath, only send it to the other end of the room, and to have a discussion cooly waived when you feel that justice is all on your own side is even more exasperating in marriage than in philosophy.

***

She leaned her head back against the window-frame, and laid her hand on the dog's head; for though, as we know, she was not fond of pets that must be held in the hands or trodden on, she was always attentive to the feelings of dogs, and very polite if she had to decline their advances.

***

But Duty has a trick of behaving unexpectedly - something like a heavy friend whom we have amiably asked to visit us, and who breaks his leg within our gates.

***

It is true Lydgate [a doctor] was constantly visiting the homes of the poor and adjusting his prescriptions of diet to their small means; but, dear me! - has it not by this time ceased to be remarkable - is it not rather what we expect in men, that they should have numerous strands of experience lying side by side and never compare them with each other? Expenditure - like ugliness and errors - becomes a totally new thing when we attach our own personality to it, and measure it by that wide difference which is manifest (in our own sensations) between ourselves and others.

***

The spiritual kind of rescue was a genuine need with [Bulstrode]. There may be coarse hypocrites, who consciously affect beliefs and emotions for the sake of gulling the world, but Bulstrode was not one of them. He was simply a man whose desires had been stronger than his theoretic beliefs, and who had gradually explained the gratification of his desires into satisfactory agreement with those beliefs. If this be hypocrisy, it is a process which shows itself occasionally in us all, to whatever confession we belong, and whether we belief in the future perfection of our race or in the nearest date fixed for the end of the world; whether we regard the earth as a putrefying nidus for a saved remnant, including ourselves, or have a passionate belief in the solidarity of mankind.

***

I think any hardship is better than pretending to do what one is paid for, and never really doing it.

***

There is no general doctrine which is not capable of eating out our morality if unchecked by the deep-seated habit of direct fellow-feeling with individual fellow-men.

So there you have it, folks: Tam's guide to Middlemarch.