I am not really a fan of most teriyaki sauces, but I wanted to learn to make an easy Asian sauce from scratch, so I looked up teriyaki sauce recipes and chose one that seemed simple and (possibly) canonical. I then made a stir-fry.
I sauteed a pound of boneless, skinless chicken thighs, a ton of broccoli, two bundles of green onions, and a chopped-up carrot in sesame oil. The sauce I made was:
slightly less than 1/2 cup soy sauce [because I ran out]
slightly less than 1/2 cup mirin (Chinese rice wine, but sold as a condiment type of thing in the grocery store, so probably not actually alcoholic)
2 tbsp brown sugar
The sauce ingredients I just warmed up in a small sauce pan. When they got hot I added some water to make what I thought would be the right amount of sauce, and a bit later I tried to thicken it with a little cornstarch, but that didn't seem to work.
I did not like how the teriyaki sauce smelled, so I was a bit apprehensive about trying it. In fact, I intended to have it for lunches, so I put away all of the portions (it made four servings, with brown rice) without even trying it. I did give a tiny sample to Ed, who pronounced it, "OK."
Tonight I had my first portion and, man, it is actually pretty terrific. The teriyaki I made is a completely adequate stir-fry sauce with none of the qualities that make me sometimes dislike teriyaki. It's sweet but not too sweet, salty but not overwhelming, and it doesn't have that kind of bitter soy sauce taste.
Monday, August 31, 2009
Awkward Writing
This morning my RSS feed for the Denver Post had the first couple of sentences of an article, "Denver computer guru gives a crash course on PC care":
They have been around for decades, and the American consumer has become completely accustomed to life with a personal computer. So why is it, then, that we keep screwing them up and, in the process, our lives?Is it just me or is that, if not quite ungrammatical, at least gruesomely awkward?
Sunday, August 30, 2009
Achingly Good
 I made red beans & rice this weekend, and it was a bit special. The kidney beans were organic, from a bin at Whole Foods, which I mention only because they were a much brighter red color than the ones I usually buy (I noticed this before cooking them) and because the beans seem to have a crazy good taste, a really concentrated earthy flavor.
I made red beans & rice this weekend, and it was a bit special. The kidney beans were organic, from a bin at Whole Foods, which I mention only because they were a much brighter red color than the ones I usually buy (I noticed this before cooking them) and because the beans seem to have a crazy good taste, a really concentrated earthy flavor.More unusually, the sausage I used is wild boar smoked sausage from Broken Arrow Ranch. I was curious what it would taste like, and what it tastes like is very lean pork sausage with a little bit of extra...fruitiness? It definitely has an extra flavor, but that flavor is not gamey or musky at all. I think "fruity" is the best I can do.
Whether because of the beans, or the sausage, or the brown basmati rice, or maybe I just did a better job with seasonings than usual, the red beans & rice came out as the best I've had in a long time. My last few pots have tended to be a bit bland, but this one is to die for. I might literally die eating it.
(Ed, unprompted, agreed that it was fantastic, far superior to my usual, so I don't think I'm only imagining the improvement.)
Saturday, August 29, 2009
Excitable
 I am really quite an excitable person.
I am really quite an excitable person.A couple of weeks ago, when I was excitedly waiting for school to start, I was thinking of all the years I have started school - 13 years of kindergarten through high school, 7 or 8 semesters at Rice, a couple of semesters at HCC, and about 25 semesters (including summers) at Metro.
With the possible exception of kindergarten, which I can't remember, I have never not been excited to start school. I have never not been excited both to start school, and about little details of starting school. The new pencil box. The blank paper. The freshly sharpened pencils. The locker! Living in a dorm! Advanced Calculus!!
And, looking back at all those times, I don't feel in retrospect that the excitement was misplaced or silly. I don't look back at my 10-year-old self, about to start 6th grade, excited about now being in middle school, and think the excitement was wrong, or that the whole thing turned out to suck after all. Because I am still the same way, it's like a continuous thread connects me to my 6th-grader self.
Although school is very salient, I am basically this way about nearly everything that I have to wait for. A new job, a doctor's appointment, a visiting friend, the next episode of a TV show - I get excited about anything. (No wonder I'm not very patient.)
I'm like a dog, except blessed (cursed?) with the ability to think about the future.
Thursday, August 27, 2009
Convergent Sequences
I'm going to explain the math from last night's calculus class here. It shouldn't be too ridiculously hard to follow, if you're interested. I was impressed by our professor's finding of ways to explain it that made a lot of sense, because this is the kind of thing that, if I were reading it in a textbook, I would balk at.
So, a sequence is just some set of numbers that happen in a particular order, for instance, the Fibonacci sequence:
1, 1, 2, 3, 5, 8, 13, ...
It's not just a set of numbers, because the order matters. The 4th number of the Fibonacci sequence is 3. You could say f(4) = 3 if you wanted to talk about the sequence as a function. You could calculate the nth term of the sequence for any n.
The simple, intuitive definition of what it means for a sequence to "converge" on some value, a, is that, as the sequence goes on, it gets closer and closer to a. But there are a couple of problems that keep this from being a usable definition:
1. Consider a sequence like this:
2. Consider a sequence like this:
Again, this sequence is converging to 1, but it doesn't seem like it's getting "closer and closer" to 1. It's oscillating around 1, with the oscillations getting smaller and smaller, but at any given point it might be moving away from 1.
So, let's move towards a more formal definition. If we consider the terms of the sequence as successive approximations of the value to which it is converging, then the question is this - can we get the approximation as good as we want?
That is, for some acceptable level of error (ε), can we find an N such that anything past the Nth term of the sequence is within ε of our value, a? If so, then the series converges to a.
It can't just be proving that some term or other is within ε of a. We might be running a computer program that provides these successive approximations, and we certainly don't want to get a worse estimate if we let the computer run too long.
And we have to be able to do this for any ε someone gives us, as long as it's greater than 0. If you say you want something with 0.00001 of a, I have to be able to say, well, anything past the 2000th value will be that close.
So there you go: convergent sequences with ε (δ comes later).
So, a sequence is just some set of numbers that happen in a particular order, for instance, the Fibonacci sequence:
1, 1, 2, 3, 5, 8, 13, ...
It's not just a set of numbers, because the order matters. The 4th number of the Fibonacci sequence is 3. You could say f(4) = 3 if you wanted to talk about the sequence as a function. You could calculate the nth term of the sequence for any n.
The simple, intuitive definition of what it means for a sequence to "converge" on some value, a, is that, as the sequence goes on, it gets closer and closer to a. But there are a couple of problems that keep this from being a usable definition:
1. Consider a sequence like this:
2, 3/2, 4/3, 5/4, 6/5, 7/6, 8/7, 9/8, 10/9, ...It seems like it's converging to 1. It's certainly getting closer and closer to 1 as it goes on. But it's also, technically, getting closer and closer to 0. So it's not enough that it gets closer and closer - it also has to get close. This series looks like it's going to get arbitrarily close to 1, which it's not going to do with 0.
2. Consider a sequence like this:
2, 1, -1.9, 1, 1.8, 1, -1.7, 1, 1.6, 1, -1.5, 1, 1.4, 1, -1.3, 1, ...
Again, this sequence is converging to 1, but it doesn't seem like it's getting "closer and closer" to 1. It's oscillating around 1, with the oscillations getting smaller and smaller, but at any given point it might be moving away from 1.
So, let's move towards a more formal definition. If we consider the terms of the sequence as successive approximations of the value to which it is converging, then the question is this - can we get the approximation as good as we want?
That is, for some acceptable level of error (ε), can we find an N such that anything past the Nth term of the sequence is within ε of our value, a? If so, then the series converges to a.
It can't just be proving that some term or other is within ε of a. We might be running a computer program that provides these successive approximations, and we certainly don't want to get a worse estimate if we let the computer run too long.
And we have to be able to do this for any ε someone gives us, as long as it's greater than 0. If you say you want something with 0.00001 of a, I have to be able to say, well, anything past the 2000th value will be that close.
So there you go: convergent sequences with ε (δ comes later).
Wednesday, August 26, 2009
Tuesday, August 25, 2009
The Well-Ordering Principle and the Pop Quiz Paradox
Last night in class, we went over a proof of the Well-Ordering Principle, and tonight, it occurs to me how much that proof reminds me of what was possibly the first inductive "proof" I ever encountered: the pop-quiz paradox.
First, the well-ordering principle. This just states that, if you have a non-empty set of natural numbers, it has a least element. The natural numbers, N, are these ones:
{1, 2, 3, ...}
i.e., the counting numbers.
So if you take any subset of those, it will have a smallest element. Duh, right?
The well-ordering principle is actually equivalent to the principle of mathematical induction, which enables a certain type of proof, which is the type I am going to give of the well-ordering principle, as follows:
Now, the pop quiz paradox:
First, the well-ordering principle. This just states that, if you have a non-empty set of natural numbers, it has a least element. The natural numbers, N, are these ones:
{1, 2, 3, ...}
i.e., the counting numbers.
So if you take any subset of those, it will have a smallest element. Duh, right?
The well-ordering principle is actually equivalent to the principle of mathematical induction, which enables a certain type of proof, which is the type I am going to give of the well-ordering principle, as follows:
Let S be a non-empty subset of the natural numbers.That is what is called a "proof by induction."
Assume, for a contradiction, that S has no least element.
Then 1 can't be in S, because otherwise, since 1 is the smallest natural number, it would be the least element of S.
Suppose, for some number k, that all of the numbers {1, 2, 3, ... k} are not in the set.
Then k+1 can't be in the set, or it would be the least element.
Thus, by the principle of mathematical induction, S is empty, a contradiction.
Now, the pop quiz paradox:
Let's say a teacher says she is going to give a pop quiz next week. It is impossible for the teacher to give a pop quiz in a specific week without the students' knowing what day it will be on. If she waits until Friday, the students will know it must be on Friday since it hasn't happened yet, so Friday is out. But since Friday is out, Thursday is also out - if she hasn't given it by Thursday, the students will know it must be on Thursday. But if Thursday and Friday are both out, then so is Wednesday, ...It is worth noting that, while the well-ordering principle is true, it is, empirically speaking, not impossible to give a pop quiz, even with advance notice of the week in which it is to occur.
Sunday, August 23, 2009
School Tidbits
Being in school again has made me feel incredibly alive, happy, and full of excitement. It is like the very air bristles with energy around me. It's amazing. I felt that I was a little depressed over the summer, and the change back has confirmed and strengthened that observation.
I got my first linear algebra assignment done Friday night; it was pretty straightforward. This morning (Saturday), I got my calculus assignment done. These are due Thursday and Wednesday, respectively.
I wanted to put more effort into calculus because the class kind of scares me and this week a lot of axioms and properties of inequalities and absolute values were floating around, so, after I finished the part of the assignment that isn't to be turned in, I wrote up the axioms he gave us for inequalities, and then each theorem he listed, and I proved each theorem according to the axioms. They weren't difficult proofs at all, but I feel much better having done them.
Later, Ed and I talked fairly extensively about the axioms and theorems. Dr. P hadn't given the axioms very rigorously and we discussed things like whether an "or" in a certain place was exclusive or not, and what the consequences of making either choice would be, and how things would change if we left out or changed other elements of the system. That was crazily fun and also, I think, productive.
(One of the theorems I proved is that 1 > 0. What a relief.)
Anyway, it's amazing to feel this way again. Even though I'm a bit more tired because of going to school four nights a week, I think I am overall much more energetic as a result of being engaged and unbored, which trumps a little extra time away from home every night.
Whoosh!
I got my first linear algebra assignment done Friday night; it was pretty straightforward. This morning (Saturday), I got my calculus assignment done. These are due Thursday and Wednesday, respectively.
I wanted to put more effort into calculus because the class kind of scares me and this week a lot of axioms and properties of inequalities and absolute values were floating around, so, after I finished the part of the assignment that isn't to be turned in, I wrote up the axioms he gave us for inequalities, and then each theorem he listed, and I proved each theorem according to the axioms. They weren't difficult proofs at all, but I feel much better having done them.
Later, Ed and I talked fairly extensively about the axioms and theorems. Dr. P hadn't given the axioms very rigorously and we discussed things like whether an "or" in a certain place was exclusive or not, and what the consequences of making either choice would be, and how things would change if we left out or changed other elements of the system. That was crazily fun and also, I think, productive.
(One of the theorems I proved is that 1 > 0. What a relief.)
Anyway, it's amazing to feel this way again. Even though I'm a bit more tired because of going to school four nights a week, I think I am overall much more energetic as a result of being engaged and unbored, which trumps a little extra time away from home every night.
Whoosh!
Friday, August 21, 2009
A Bit More About Liking Math
I should clarify my previous post thusly:
1. I do find the material of math interesting. Unlike psychology or economics, I'm not usually actually curious about math. I certainly don't feel curious about unresolved problems in math. But once I see what's there, I do tend to really enjoy it. So in terms of interest, math is maybe like art for me. I'm not actually curious to see new art, but if I find myself in a gallery I will often super enjoy what I find there.
2. Is math a relative weakness for me? My best guess is that it's somewhere in the middle of my talents. But it may be only that I have gotten far enough in math to see my own limitations, while only skimming the surface of other subjects. It may be that I only imagine that I would kick more ass in some other field. I find that quite plausible. Also, of course, the nature of math is such that it's somewhat objective whether you're succeeding or failing. I might be able to wrongly believe that my essay on Macbeth is a work of genius, but a proof either works or it doesn't.
3. Do I prefer subjects I fear failing at? Perhaps not. I think it's more likely that my disinclination to work means that I'm more likely to work hard if I'm moderately afraid than if I'm pretty confident, and of course, as I've mentioned before, more work = more enjoyment, at least for me. (Is this true for other people? Do you prefer a difficult 2-hour hike to an easy one, after it's all over?) There is also kind of no superficial level of math. You can read a book like How the Mind Works and feel like you have a grasp of cognitive psychology, but even the equivalent lay math book will require work and thought to grasp (again, at least for me). You either work hard and get something out of it or you don't and...don't.
So I guess what I'm saying is, contra modern wisdom, all-or-nothing thinking and a slight lack of self-efficacy are drivers of my math success.
1. I do find the material of math interesting. Unlike psychology or economics, I'm not usually actually curious about math. I certainly don't feel curious about unresolved problems in math. But once I see what's there, I do tend to really enjoy it. So in terms of interest, math is maybe like art for me. I'm not actually curious to see new art, but if I find myself in a gallery I will often super enjoy what I find there.
2. Is math a relative weakness for me? My best guess is that it's somewhere in the middle of my talents. But it may be only that I have gotten far enough in math to see my own limitations, while only skimming the surface of other subjects. It may be that I only imagine that I would kick more ass in some other field. I find that quite plausible. Also, of course, the nature of math is such that it's somewhat objective whether you're succeeding or failing. I might be able to wrongly believe that my essay on Macbeth is a work of genius, but a proof either works or it doesn't.
3. Do I prefer subjects I fear failing at? Perhaps not. I think it's more likely that my disinclination to work means that I'm more likely to work hard if I'm moderately afraid than if I'm pretty confident, and of course, as I've mentioned before, more work = more enjoyment, at least for me. (Is this true for other people? Do you prefer a difficult 2-hour hike to an easy one, after it's all over?) There is also kind of no superficial level of math. You can read a book like How the Mind Works and feel like you have a grasp of cognitive psychology, but even the equivalent lay math book will require work and thought to grasp (again, at least for me). You either work hard and get something out of it or you don't and...don't.
So I guess what I'm saying is, contra modern wisdom, all-or-nothing thinking and a slight lack of self-efficacy are drivers of my math success.
Thursday, August 20, 2009
Fear of Failure
I often talk about liking math, but what is more true is that math keeps me energized and excited to keep pursuing it. And I think part of the reason for that is that, with math I have a genuine fear of failure.
I was sitting in my calculus class last night feeling a familiar mixture of slight despair and worry over the material. It's not that it's hard, exactly. It just suggests that horrible things are coming down the pike, for which I will need the slightly scary stuff I'm working on right now. Am I smart enough for this class?
I mean, yes, I am. I must be. I am almost certainly above average in my class, likely in the top quarter. If most people are going to pass this class then I can do well in it.
That's what logic tells me, but it's not how I feel.
If I were taking a 400-level English class, there would be no doubt in my mind that if I put in a reasonable amount of effort, I would absolutely kill it. Ditto History, or any other subject that relies on knowledge, reading, and the manipulation of ideas. And I think that feeling of certainty - the very strong linkage between work and outcome - tends to make me a bit lax and uninterested.
Obviously I am also unmotivated by feeling that no effort of mine can make a difference. Set me at the start of a marathon and you won't see me trying. But I think the thrill and fear of not knowing whether I can do math (whatever math is before me) keeps me going, keeps me trying, keeps me signing up for more courses.
This explains why I'm majoring in something that isn't, honestly, a great strength for me.
I was sitting in my calculus class last night feeling a familiar mixture of slight despair and worry over the material. It's not that it's hard, exactly. It just suggests that horrible things are coming down the pike, for which I will need the slightly scary stuff I'm working on right now. Am I smart enough for this class?
I mean, yes, I am. I must be. I am almost certainly above average in my class, likely in the top quarter. If most people are going to pass this class then I can do well in it.
That's what logic tells me, but it's not how I feel.
If I were taking a 400-level English class, there would be no doubt in my mind that if I put in a reasonable amount of effort, I would absolutely kill it. Ditto History, or any other subject that relies on knowledge, reading, and the manipulation of ideas. And I think that feeling of certainty - the very strong linkage between work and outcome - tends to make me a bit lax and uninterested.
Obviously I am also unmotivated by feeling that no effort of mine can make a difference. Set me at the start of a marathon and you won't see me trying. But I think the thrill and fear of not knowing whether I can do math (whatever math is before me) keeps me going, keeps me trying, keeps me signing up for more courses.
This explains why I'm majoring in something that isn't, honestly, a great strength for me.
Wednesday, August 19, 2009
First Day(s) of School
This semester, I have two 4-credit-hour classes, and they take place on different nights. My schedule is
It's inconvenient to have to travel to campus four times a week, but nice to only have two hours of class when I go (thus no temptation to skip the second class). And I initially thought the late hours would suck, but I've changed my work schedule so that I work 9:30-6:30 and just shifted my whole day later.
This also means I get up after Ed has left for work, and get home around his bedtime, so most of my time at home during the week will be alone. It's only been two days, but I've basically enjoyed it so far. I'm sure I'll enjoy seeing him on the weekends.
Anyway, I have been to both classes, so here are my thoughts so far.
Linear Algebra
The professor was friendly, very casually dressed, and just slightly spacy. I feel a little concerned that she won't make the class theoretical/"proofy" enough, but by the end of class I thought that she would. At some point, I wrote, on the edge of my paper that I save for comments, "Please go into the algebra of this," because one of the errors I made last time I did this was to focus too much on the algorithms of manipulating matrices and not enough on the underlying algebra. Immediately once I had written it she went into a long bit about the algebra of what we were doing. Nice.
This class is in the building right next to where I usually park, so that's convenient, but it's in an uncomfortable classroom - crowded, noisy, and with the one-piece desks that I don't like. So it is not a very desirable place to be for two hours.
We'll have two tests, a final, homework, quizzes, and class participation. She takes attendance and apparently cares if you show up. She also said there would be a lot of working together in groups, which I utterly dread, because (a) yuck, groups, ugh, but also (b) trying to move desks around in a totally packed classroom of one-piece desks sucks.
So I guess I'm giving this class mixed reviews so far. We have homework due next week that is almost all from the high-numbered problems in the textbook, so that's good.
Advanced Calculus I
If you're wondering what this class is, it is sometimes also called "Real Analysis" (which is to say, analysis of the real numbers, not real as in genuine). You could also say it is the "continuous math" to go along with my "discrete math" from a few semesters ago.
The professor is a slight, unassuming Brit with the obligatory charming accent. He told us that this is the hardest class in undergrad, but also the best, and assured us that it does not exist solely in order to keep you from getting into graduate school.
He also said the class is about three things:
I'm enjoying this class so far. I spent an hour last night working on our first homework, which was reasonably challenging and fun. One of the problems we had was several statements that we had to negate - math equivalents of things like
The class is also held in a classroom with long tables and regular rolling-type desk chairs, so it's very comfortable to be in for two hours.
We'll be having three exams plus a final, homework counts as 30% of the grade, and there is no paper, project, or threat of group work.
So that's how my semester looks so far.
| M/W | 7:00-8:50pm | Advanced Calculus I |
| T/R | 7:00-8:50pm | Linear Algebra |
This also means I get up after Ed has left for work, and get home around his bedtime, so most of my time at home during the week will be alone. It's only been two days, but I've basically enjoyed it so far. I'm sure I'll enjoy seeing him on the weekends.
Anyway, I have been to both classes, so here are my thoughts so far.
Linear Algebra
The professor was friendly, very casually dressed, and just slightly spacy. I feel a little concerned that she won't make the class theoretical/"proofy" enough, but by the end of class I thought that she would. At some point, I wrote, on the edge of my paper that I save for comments, "Please go into the algebra of this," because one of the errors I made last time I did this was to focus too much on the algorithms of manipulating matrices and not enough on the underlying algebra. Immediately once I had written it she went into a long bit about the algebra of what we were doing. Nice.
This class is in the building right next to where I usually park, so that's convenient, but it's in an uncomfortable classroom - crowded, noisy, and with the one-piece desks that I don't like. So it is not a very desirable place to be for two hours.
We'll have two tests, a final, homework, quizzes, and class participation. She takes attendance and apparently cares if you show up. She also said there would be a lot of working together in groups, which I utterly dread, because (a) yuck, groups, ugh, but also (b) trying to move desks around in a totally packed classroom of one-piece desks sucks.
So I guess I'm giving this class mixed reviews so far. We have homework due next week that is almost all from the high-numbered problems in the textbook, so that's good.
Advanced Calculus I
If you're wondering what this class is, it is sometimes also called "Real Analysis" (which is to say, analysis of the real numbers, not real as in genuine). You could also say it is the "continuous math" to go along with my "discrete math" from a few semesters ago.
The professor is a slight, unassuming Brit with the obligatory charming accent. He told us that this is the hardest class in undergrad, but also the best, and assured us that it does not exist solely in order to keep you from getting into graduate school.
He also said the class is about three things:
- The nature of the reals and their relationship to the rationals
- ε's and δ's and proofs of everything in calculus
- 19th century mathematics
I'm enjoying this class so far. I spent an hour last night working on our first homework, which was reasonably challenging and fun. One of the problems we had was several statements that we had to negate - math equivalents of things like
For every cat, there is at least one dog over the age of 7 who has chased that cat.and more complicated ones like
There is some baby such that every woman in this household who is over 30 and of sound mind has diapered that baby.I had fun writing the negations of them, though I also felt doubt as to whether I chose the most elegant or direct methods of doing so.
The class is also held in a classroom with long tables and regular rolling-type desk chairs, so it's very comfortable to be in for two hours.
We'll be having three exams plus a final, homework counts as 30% of the grade, and there is no paper, project, or threat of group work.
So that's how my semester looks so far.
Tuesday, August 18, 2009
Review of "In Defense of Food"
I'm currently reading Michael Pollan's book In Defense of Food. Pollan is the guy who wrote The Omnivore's Dilemma (and some other books, of course) and he is basically a proponent of what you might call natural eating - eating regular food-type food that isn't too processed or industrial.
I haven't read any of his other stuff, but I'm really enjoying this book. Even though I haven't learned that much actually new material from it, he does give a different perspective, and the way he writes about food is motivational for me.
One thing he opposes is what he calls "nutritionism" - that is, the culturally prevalent practice of talking about foods as though they are just collections of chemicals that have nutritional consequences. An example he brings up is a government panel or committee of some kind in 1977 that was looking at heart disease, and decided to recommend that Americans eat less dairy and meat, since it was pretty clearly associated with increased risk of heart disease. Of course, the dairy and meat industries freaked the fuck out, and the recommendations were changed to, basically, "avoid saturated fat," even though there wasn't good evidence that saturated fat was the problematic aspect of meat and dairy. But by focusing on invisible chemical aspects of foods rather than on foods themselves, the government could make dietary recommendations without earning the wrath of any particular food industries.
The growth of nutritionism has also, in Pollan's view, fostered the industrial approach to food that has our grocery stores full of boxes and bags. Once it's discovered that antioxidants, or fiber, or Omega-3 acids are healthy, then they can be added to cereals, breads, pasta, yogurts, cookies, and all the other foods that industry churns out for us. A recommendation like "eat more fruit" or "hey how about some green veggies" doesn't foster the same kind of innovation in new products. (And in case it's not obvious, it's a lot easier to make big profits on something like cookies than on something like eggplants.)
He delves into quite a bit of nutrition science himself, a contradiction that he acknowledges. But it's not that he rejects science, including nutritional science, as our best tool to understanding what makes some foods healthier than others. What he rejects is using today's limited science to decide what to eat based on a nutritional perspective. (He's also in favor of the idea that people can suffer from "orthorexia," or an obsession with the healthfulness of foods.)
What's clear to Pollan is that the basic culprit behind the diseases of affluence (obesity, heart disease, diabetes, cancer, etc.) is (besides the small contributing factor of longevity) basically the Western Diet itself. Whenever people living on any kind of traditional diet (of which there are quite diverse kinds in the world) change over to a Western diet they get fat and diabetic and all the rest of it.
So his basic advice is, don't eat the Western diet. He begins the book with the (familiar) advice: "Eat food. Mostly plants. Not too much." The last third (perhaps) of the book is devoted to ideas about how to do this - what he calls "algorithms" and I would call "heuristics." He talks about each part separately - what is "food" (vs. a "foodlike product")? What kind of plants are best to eat (lots of variety; more leaves than seeds)? And what kind of cultures of eating should we follow in order to make food healthy as well as emotionally and socially satisfying?
If I lived fully in accordance with my most basic feelings, I would eat like most of my dad's side of the family eats - a lot of fried chicken and other fast food, chain restaurant fare, the occasional home-cooked spaghetti or hamburger. Most of the other side of my family eat a pretty impressive diet of vegetarian (or near-vegetarian), fresh, from-scratch, vegetable-heavy foods - to such an extent that, while I admire it, it's also hard for me to understand how they can do it. And, of course, my dad's side of my family is markedly more obese and has vastly more health problems than my mom's side.
(My Aunt - my mom's sister - tells a story about when I was little. I visited her during the summer, and she had made some beautiful fresh gazpacho from things she had grown in her own garden. When I went home, I told my mom, "...and all we had to eat was frozen tomato soup!" What's funny to me about the story, and about my Aunt's telling it, is that I would feel exactly the same way now if someone served me gazpacho as a meal.)
So I am kind of trying to use education and knowledge to move myself from my western-diet nature (which has me end up like my dad's family) to a diet more like that of my mom's family (which will help me live longer and in better health). I mean, to be clear, I don't think the difference between the two sides of my family is innate - like genetic or whatever. But growing up as I did, in this place and time, what I want is "the good stuff" - the more fried, refined, salted, sweetened, and processed the better.
So I think Michael Pollan's basis thesis is right, and I am finding the book reasonably motivational. (Some of his stuff also reminded me of Sally's hypothetical Navajo talk about eating.) I recommend reading it, and it also makes a very good companion (obviously up the same alley, yet without much overlap) to The End of Overeating.
I haven't read any of his other stuff, but I'm really enjoying this book. Even though I haven't learned that much actually new material from it, he does give a different perspective, and the way he writes about food is motivational for me.
One thing he opposes is what he calls "nutritionism" - that is, the culturally prevalent practice of talking about foods as though they are just collections of chemicals that have nutritional consequences. An example he brings up is a government panel or committee of some kind in 1977 that was looking at heart disease, and decided to recommend that Americans eat less dairy and meat, since it was pretty clearly associated with increased risk of heart disease. Of course, the dairy and meat industries freaked the fuck out, and the recommendations were changed to, basically, "avoid saturated fat," even though there wasn't good evidence that saturated fat was the problematic aspect of meat and dairy. But by focusing on invisible chemical aspects of foods rather than on foods themselves, the government could make dietary recommendations without earning the wrath of any particular food industries.
The growth of nutritionism has also, in Pollan's view, fostered the industrial approach to food that has our grocery stores full of boxes and bags. Once it's discovered that antioxidants, or fiber, or Omega-3 acids are healthy, then they can be added to cereals, breads, pasta, yogurts, cookies, and all the other foods that industry churns out for us. A recommendation like "eat more fruit" or "hey how about some green veggies" doesn't foster the same kind of innovation in new products. (And in case it's not obvious, it's a lot easier to make big profits on something like cookies than on something like eggplants.)
He delves into quite a bit of nutrition science himself, a contradiction that he acknowledges. But it's not that he rejects science, including nutritional science, as our best tool to understanding what makes some foods healthier than others. What he rejects is using today's limited science to decide what to eat based on a nutritional perspective. (He's also in favor of the idea that people can suffer from "orthorexia," or an obsession with the healthfulness of foods.)
What's clear to Pollan is that the basic culprit behind the diseases of affluence (obesity, heart disease, diabetes, cancer, etc.) is (besides the small contributing factor of longevity) basically the Western Diet itself. Whenever people living on any kind of traditional diet (of which there are quite diverse kinds in the world) change over to a Western diet they get fat and diabetic and all the rest of it.
So his basic advice is, don't eat the Western diet. He begins the book with the (familiar) advice: "Eat food. Mostly plants. Not too much." The last third (perhaps) of the book is devoted to ideas about how to do this - what he calls "algorithms" and I would call "heuristics." He talks about each part separately - what is "food" (vs. a "foodlike product")? What kind of plants are best to eat (lots of variety; more leaves than seeds)? And what kind of cultures of eating should we follow in order to make food healthy as well as emotionally and socially satisfying?
If I lived fully in accordance with my most basic feelings, I would eat like most of my dad's side of the family eats - a lot of fried chicken and other fast food, chain restaurant fare, the occasional home-cooked spaghetti or hamburger. Most of the other side of my family eat a pretty impressive diet of vegetarian (or near-vegetarian), fresh, from-scratch, vegetable-heavy foods - to such an extent that, while I admire it, it's also hard for me to understand how they can do it. And, of course, my dad's side of my family is markedly more obese and has vastly more health problems than my mom's side.
(My Aunt - my mom's sister - tells a story about when I was little. I visited her during the summer, and she had made some beautiful fresh gazpacho from things she had grown in her own garden. When I went home, I told my mom, "...and all we had to eat was frozen tomato soup!" What's funny to me about the story, and about my Aunt's telling it, is that I would feel exactly the same way now if someone served me gazpacho as a meal.)
So I am kind of trying to use education and knowledge to move myself from my western-diet nature (which has me end up like my dad's family) to a diet more like that of my mom's family (which will help me live longer and in better health). I mean, to be clear, I don't think the difference between the two sides of my family is innate - like genetic or whatever. But growing up as I did, in this place and time, what I want is "the good stuff" - the more fried, refined, salted, sweetened, and processed the better.
So I think Michael Pollan's basis thesis is right, and I am finding the book reasonably motivational. (Some of his stuff also reminded me of Sally's hypothetical Navajo talk about eating.) I recommend reading it, and it also makes a very good companion (obviously up the same alley, yet without much overlap) to The End of Overeating.
Monday, August 17, 2009
Why I (Sometimes) Choose Organic
Yesterday, the friends we have over every other weekend asked me something like, "Why are you obsessed with organic?" They've noticed that the snacks I bring out when they come over tend to be organic rather than conventional junk food, which is always a bit odd (is it really healthier to eat a Newman-O rather than an Oreo?) And Ed chimed in to point out that I drink organic milk.
The vast majority of the food I eat is not organic, especially because I eat quite a lot of restaurant food, but I do choose organic foods relatively often.
With regards to agriculture and sustainability, I don't know what the answer is. I know that eating less meat, especially less beef, is the biggest step you can take towards lowering the environmental footprint of what you eat. Both conventional crops - which require vast amount of petroleum and other limited resources to produce - and organic crops - which require more land per unit of production - have sustainability problems. I think in general this aspect tips towards organic only because the people who buy organic tend to be more environmentally minded and are thus working on and paying attention to these issues. (I also don't think there is any risk that suddenly all of America is going to eat mostly organic foods and thus we'll have to convert a lot more land to growing crops.)
All things being equal, I would rather not eat pesticide, herbicide, etc., residue. I think the amount of that stuff in our food is actually very small and quite safe, but I admit that the idea of not having it on my food does appeal to me.
I often choose organic (or organic-related) dairy and eggs because those practices tend to be associated with less animal cruelty. But again, most of the dairy and egg products I eat are from restaurants, where I exercise no control over how the animals are treated.
Although I haven't proceeded very far in this direction, I am trying to trend towards eating more natural, whole foods. I would like to cultivate in myself the idea that eating a bag full of cheap corn derivatives and chemicals (e.g., oreos) is unappealing. I'd also like to feel that a hyperpalatable, overly-engineered food like southwestern egg rolls from Chili's is gross rather than delicious. Because people who hold these values often choose organic foods, organic prepared or semi-prepared foods tend to reflect these values. So even though I doubt Newman-O's are actually healthier than Oreos, if you read the ingredients you will find mostly things you would cook with yourself. Here, in fact, are the ingredients for Newman-O's:
I want to eat things that are more like things you would make and less like things invented in a factory, and I find that choosing organic encourages me to develop that aesthetic.
So, in short, my reasons for choosing organic are mostly these:
The vast majority of the food I eat is not organic, especially because I eat quite a lot of restaurant food, but I do choose organic foods relatively often.
With regards to agriculture and sustainability, I don't know what the answer is. I know that eating less meat, especially less beef, is the biggest step you can take towards lowering the environmental footprint of what you eat. Both conventional crops - which require vast amount of petroleum and other limited resources to produce - and organic crops - which require more land per unit of production - have sustainability problems. I think in general this aspect tips towards organic only because the people who buy organic tend to be more environmentally minded and are thus working on and paying attention to these issues. (I also don't think there is any risk that suddenly all of America is going to eat mostly organic foods and thus we'll have to convert a lot more land to growing crops.)
All things being equal, I would rather not eat pesticide, herbicide, etc., residue. I think the amount of that stuff in our food is actually very small and quite safe, but I admit that the idea of not having it on my food does appeal to me.
I often choose organic (or organic-related) dairy and eggs because those practices tend to be associated with less animal cruelty. But again, most of the dairy and egg products I eat are from restaurants, where I exercise no control over how the animals are treated.
Although I haven't proceeded very far in this direction, I am trying to trend towards eating more natural, whole foods. I would like to cultivate in myself the idea that eating a bag full of cheap corn derivatives and chemicals (e.g., oreos) is unappealing. I'd also like to feel that a hyperpalatable, overly-engineered food like southwestern egg rolls from Chili's is gross rather than delicious. Because people who hold these values often choose organic foods, organic prepared or semi-prepared foods tend to reflect these values. So even though I doubt Newman-O's are actually healthier than Oreos, if you read the ingredients you will find mostly things you would cook with yourself. Here, in fact, are the ingredients for Newman-O's:
Organic Unbleached Flour, Organic Sugar, Powdered Sugar, Organic Palm Oil, Canola Oil (Expeller Pressed), Organic Cocoa, Cocoa (Processed with Alkali), Organic Unsweetened Chocolate, Natural Flavor, Salt, Sodium Bicarbonate, Soy Lecithin, (an Emulsifier)and for Oreos:
Sugar, Enriched Flour, High Oleic Canola Oil and/or Palm Oil and/or Canola Oil and/or Soybean Oil, Cocoa (Processed with Alkali), High Fructose Corn Syrup, Cornstarch, Leavening (Baking Soda and/or Calcium Phosphate), Salt, Soy Lecithin (Emulsifier), Vanillin - An Artificial Flavor, ChocolateThose are not actually as different as I'd anticipated, but this trend does exist in general.
I want to eat things that are more like things you would make and less like things invented in a factory, and I find that choosing organic encourages me to develop that aesthetic.
So, in short, my reasons for choosing organic are mostly these:
- reduced animal cruelty
- not eating pesticide residue
- possible long-term land use, sustainability, and environmental benefits
- encouraging in myself a preference for natural, whole foods
Tuesday, August 11, 2009
Fewer Rights?
Over at the Atlantic, David Indiviglio is arguing that credit card companies are responding to a new law intended to increase debtors' rights by actually removing one of those rights:
I completely fail to see how this is a diminishment of my rights (even taking "rights" in a pretty loose sense). I never actually thought I had the "right" to go over my limit; I thought it was basically a screw-up when it happened, and then I would be penalized. I mean, it's the same thing (in my mind) as overdrawing your bank account - it can happen, but it's not something you're really "allowed" to do, hence the penalty.
I certainly prefer that the transaction is either declined, or accepted with no additional fee.
Are there people who viewed the ability to go over their credit limit in return for paying a penalty as a good thing, a service they enjoyed using?
The New York Times reports one of the early casualties of Congress' recent credit card "bill of rights" legislation. A few prominent credit card companies are actually taking a right away from many in response to the new regulation: the right to exceed your credit limit.Basically, the law apparently says that credit card companies can't charge you a fee for going over your limit unless you specifically ask for permission to do so and agree to the fee. Discover and American Express have responded by changing their system so that if you try to go over your limit, the transaction is either declined, or accepted with no fee. (They didn't want to go through the hassle of implementing a system whereby one could request permission and agree to a fee.)
...
How did [Discover and American Express] do it? Easy. They eliminated their cardholders' ability to purchase anything that would put them over their credit limit, unless the companies allow them to do so for no additional fee. After all, those who cannot breach their limit will never need to pay the fee.
I completely fail to see how this is a diminishment of my rights (even taking "rights" in a pretty loose sense). I never actually thought I had the "right" to go over my limit; I thought it was basically a screw-up when it happened, and then I would be penalized. I mean, it's the same thing (in my mind) as overdrawing your bank account - it can happen, but it's not something you're really "allowed" to do, hence the penalty.
I certainly prefer that the transaction is either declined, or accepted with no additional fee.
Are there people who viewed the ability to go over their credit limit in return for paying a penalty as a good thing, a service they enjoyed using?
Thursday, August 06, 2009
Praxis II Mathematics Subject Exam
If I decide to try to get alternative certification as a teacher, I will most likely need to take the Praxis II Mathematics subject exam, which is another one by ETS (like the SAT, GRE, etc.) Some states (like Texas) don't take this, and some states (like Colorado) take either this or their own in-state exam, but many states do take the Praxis.
So, out of curiosity, I downloaded a complete sample exam and took it. It is on paper (it's not one of those computer-based tests), 50 questions long, and you have two hours for it.
I won't say that it was trivial. You do need to know math in order to do well on it - at least high school math, and some college math to seal the deal. (I think I actually could have passed this when I graduated from high school, but most people wouldn't.)
I finished with about 20 minutes to spare and got 46 of the questions right, for an adjusted score of 184 (out of roughly 200). I would need a 156, which on this test corresponded to getting 32 questions right, to meet Colorado standards.
So I do feel confident that I can pass this exam without any additional study.
So, out of curiosity, I downloaded a complete sample exam and took it. It is on paper (it's not one of those computer-based tests), 50 questions long, and you have two hours for it.
I won't say that it was trivial. You do need to know math in order to do well on it - at least high school math, and some college math to seal the deal. (I think I actually could have passed this when I graduated from high school, but most people wouldn't.)
I finished with about 20 minutes to spare and got 46 of the questions right, for an adjusted score of 184 (out of roughly 200). I would need a 156, which on this test corresponded to getting 32 questions right, to meet Colorado standards.
So I do feel confident that I can pass this exam without any additional study.
Wednesday, August 05, 2009
Is Mint.com Safe?
Yesterday, I wrote about managing my money with Mint.com. Ed asked, in a comment, whether Mint.com can be trusted - is it safe to use the service? Here are my thoughts on that question.
Here is the information I have given Mint:
The only real point of danger I see here is that Mint itself has my user names, passwords, security question answers, etc., stored somewhere. This leads to two question:
1. Is Mint a criminal enterprise?
I would say not. They are so mainstream, have so many reviews from mainstream sites, so many certificates from ratings authorities, that I think we would know by now if they were criminals out to steal our money.
2. Can Mint keep my data safe from other criminals?
By this I mean, is Mint going to be hacked into by someone who will then get all of my user names and passwords and use these for nefarious purposes?
I have reasonably good faith that Mint has adequate security meaures in place to prevent this. I also know that anything you can do through accessing my online accounts takes a few days to actually generate money. (For instance, you could have a card issued to yourself from one of my credit accounts, or set yourself up as a bill pay payee and send yourself a payment, or copy the information from one of my scanned-in checks and use the account and routing number to submit your own check from my account to yourself.) I think that if a major breach happened at Mint, they would know, and enough people would be affected that we'd all know to take steps to prevent a loss.
Ultimately, whether you decide to trust systems like this is a personal question. I (briefly) lost $1300 once when someone broke into my Paypal account, but I was able to recover the money within a few days, and the hassle involved was small. Apparently some people have suffered identity theft crimes that were harder to recover from.
At the same time, using Mint makes me much more likely to notice fraud happening in any of my accounts, because it won't take a billing cycle or two to notice new charges show up on a credit card I don't use, or to spot a suspicious withdrawal from my savings account.
My guess is that, on net, using Mint is safer than not using it.
Here is the information I have given Mint:
- my email address
- the names of financial institutions I have relationships with
- the user logins and passwords for those accounts
- my name
- my address
- my phone number
- my account numbers
- my social security number
The only real point of danger I see here is that Mint itself has my user names, passwords, security question answers, etc., stored somewhere. This leads to two question:
1. Is Mint a criminal enterprise?
I would say not. They are so mainstream, have so many reviews from mainstream sites, so many certificates from ratings authorities, that I think we would know by now if they were criminals out to steal our money.
2. Can Mint keep my data safe from other criminals?
By this I mean, is Mint going to be hacked into by someone who will then get all of my user names and passwords and use these for nefarious purposes?
I have reasonably good faith that Mint has adequate security meaures in place to prevent this. I also know that anything you can do through accessing my online accounts takes a few days to actually generate money. (For instance, you could have a card issued to yourself from one of my credit accounts, or set yourself up as a bill pay payee and send yourself a payment, or copy the information from one of my scanned-in checks and use the account and routing number to submit your own check from my account to yourself.) I think that if a major breach happened at Mint, they would know, and enough people would be affected that we'd all know to take steps to prevent a loss.
Ultimately, whether you decide to trust systems like this is a personal question. I (briefly) lost $1300 once when someone broke into my Paypal account, but I was able to recover the money within a few days, and the hassle involved was small. Apparently some people have suffered identity theft crimes that were harder to recover from.
At the same time, using Mint makes me much more likely to notice fraud happening in any of my accounts, because it won't take a billing cycle or two to notice new charges show up on a credit card I don't use, or to spot a suspicious withdrawal from my savings account.
My guess is that, on net, using Mint is safer than not using it.
Stupid Health Care Tricks
As of my recent doctor visit, I am taking ranitidine (aka Zantac) to manage my heartburn. I was given a prescription for this, although it is also available over-the-counter. My prescription is for 2 pills a day, or 60 a month.
I find prescriptions kind of a pain in the ass, what with the need to renew them and everything, so as I went to the store I thought I would probably just buy them over the counter. What I found was that a 24-pack (12 day supply, in other words) of generic ranitidine was something like $6 on sale. I knew my co-pay for prescription drugs was something like $10, so I went ahead and filled the prescription.
It turns out that ranitidine is one of my pharmacy's low-cost drugs, so the entire month's supply - 60 pills, or $15 worth of OTC stuff, was $4. That wasn't dependent on my insurance, it was just the pharmacy's price.
I have seen this before, where, either because of insurance or just in general, you can get prescription drugs more cheaply than the same drugs over-the-counter.
One of the things I dislike about the way that health care works in America is that, if you don't have health insurance, you end up paying more for things, and not just in the obvious way. For instance, my doctor's fee is something like $135 for an office visit, but my insurance pays her $45. If I were uninsured I'd have to pay the full $135 because I wasn't included in that negotiated rate.
And if I couldn't afford to see a doctor about my heartburn, I'd have to pay almost four times as much for my ranitidine.
This particular thing is one of those situations where each individual component makes sense and seems like a good thing, but the overall effect is somewhat perverse.
I find prescriptions kind of a pain in the ass, what with the need to renew them and everything, so as I went to the store I thought I would probably just buy them over the counter. What I found was that a 24-pack (12 day supply, in other words) of generic ranitidine was something like $6 on sale. I knew my co-pay for prescription drugs was something like $10, so I went ahead and filled the prescription.
It turns out that ranitidine is one of my pharmacy's low-cost drugs, so the entire month's supply - 60 pills, or $15 worth of OTC stuff, was $4. That wasn't dependent on my insurance, it was just the pharmacy's price.
I have seen this before, where, either because of insurance or just in general, you can get prescription drugs more cheaply than the same drugs over-the-counter.
One of the things I dislike about the way that health care works in America is that, if you don't have health insurance, you end up paying more for things, and not just in the obvious way. For instance, my doctor's fee is something like $135 for an office visit, but my insurance pays her $45. If I were uninsured I'd have to pay the full $135 because I wasn't included in that negotiated rate.
And if I couldn't afford to see a doctor about my heartburn, I'd have to pay almost four times as much for my ranitidine.
This particular thing is one of those situations where each individual component makes sense and seems like a good thing, but the overall effect is somewhat perverse.
Tuesday, August 04, 2009
Mint.com
I've recently been experimenting with managing my accounts using Mint.com, which is free online software for just such a purpose. (They support themselves by giving you credit card, savings account, brokerage firm, etc., offers based on your particulars, under one portion of the website.) Prior to this, I've been managing some of my accounts in Excel, and some not at all.
Mint.com will automatically pull information from your checking, savings, investment, credit card, and loan acounts. (It probably doesn't work for every obscure bank and credit union, but it worked for almost all of mine. One of my 401K's that is managed through an old employer's own website did not work.) You can also enter other financially relevant things like the value of your home (which it will automatically get from some other site, if you want, once you give it the address) or car.
Once you get all of your accounts put in, the overview screen looks like this:

(You can probably get a bigger image by clicking. Also, I tried to blur particularly private areas.)
That stuff on the right is the budget that I set up. Since not many transactions have gone through for August yet, Mint isn't showing me anything about how my budget is going. So far.
The "Transactions" tab will give you output like this, which you can filter by account or in various other ways:
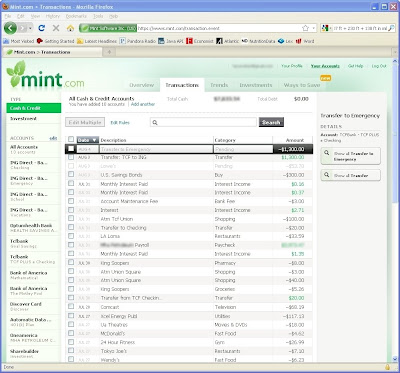
It will attempt to categorize all of your transactions for you. You can add new categories if you want, and you can also tell it to ignore certain transactions (not sure why you would do this) or to consistently rename and recategorize some. (For instance, Mint originally guessed that my monthly payment to Amica was for some kind of financial service, but now it knows it is for car insurance.)
Then you can pull up graphs of what you spend money on. This is what my graph for last month looks like. (The "Shopping" category makes it not totally useful; I've been using cash for most things, and this is how I categorized my ATM withdrawals.)
 If I click on the blue segment that represents Food & Dining, I get this sub-chart:
If I click on the blue segment that represents Food & Dining, I get this sub-chart:
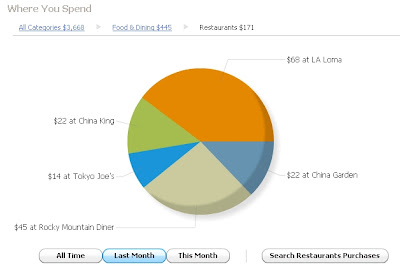
 and if I click on the green Restaurants segment, I can see exactly where I went:
and if I click on the green Restaurants segment, I can see exactly where I went:
 The site has a lot of other features as well, like charts for showing me how the various investments in my 401K plans are doing, comparisons of my spending to that of other Mint customers, and so on. Which of these are the most useful (or useful at all besides as a way to waste time at work), time will tell. But I'm enjoying it so far, and hoping it simplifies my financial life a bit.
The site has a lot of other features as well, like charts for showing me how the various investments in my 401K plans are doing, comparisons of my spending to that of other Mint customers, and so on. Which of these are the most useful (or useful at all besides as a way to waste time at work), time will tell. But I'm enjoying it so far, and hoping it simplifies my financial life a bit.
Mint.com will automatically pull information from your checking, savings, investment, credit card, and loan acounts. (It probably doesn't work for every obscure bank and credit union, but it worked for almost all of mine. One of my 401K's that is managed through an old employer's own website did not work.) You can also enter other financially relevant things like the value of your home (which it will automatically get from some other site, if you want, once you give it the address) or car.
Once you get all of your accounts put in, the overview screen looks like this:

(You can probably get a bigger image by clicking. Also, I tried to blur particularly private areas.)
That stuff on the right is the budget that I set up. Since not many transactions have gone through for August yet, Mint isn't showing me anything about how my budget is going. So far.
The "Transactions" tab will give you output like this, which you can filter by account or in various other ways:

It will attempt to categorize all of your transactions for you. You can add new categories if you want, and you can also tell it to ignore certain transactions (not sure why you would do this) or to consistently rename and recategorize some. (For instance, Mint originally guessed that my monthly payment to Amica was for some kind of financial service, but now it knows it is for car insurance.)
Then you can pull up graphs of what you spend money on. This is what my graph for last month looks like. (The "Shopping" category makes it not totally useful; I've been using cash for most things, and this is how I categorized my ATM withdrawals.)
 If I click on the blue segment that represents Food & Dining, I get this sub-chart:
If I click on the blue segment that represents Food & Dining, I get this sub-chart: and if I click on the green Restaurants segment, I can see exactly where I went:
and if I click on the green Restaurants segment, I can see exactly where I went: The site has a lot of other features as well, like charts for showing me how the various investments in my 401K plans are doing, comparisons of my spending to that of other Mint customers, and so on. Which of these are the most useful (or useful at all besides as a way to waste time at work), time will tell. But I'm enjoying it so far, and hoping it simplifies my financial life a bit.
The site has a lot of other features as well, like charts for showing me how the various investments in my 401K plans are doing, comparisons of my spending to that of other Mint customers, and so on. Which of these are the most useful (or useful at all besides as a way to waste time at work), time will tell. But I'm enjoying it so far, and hoping it simplifies my financial life a bit.
Subscribe to:
Posts (Atom)




















